E aí, guerreiro? Pronto para mais um conteúdo de Física? Depois de vermos o movimento uniforme e o movimento uniformemente variado, está na hora de ir além nos estudos. Agora, vamos incrementar o tema com as análises gráficas dos movimentos. Confira com o Estratégia Militares!
Inicialmente, vamos estudar os conceitos envolvendo os gráficos de 𝑠 × 𝑡, 𝑣 × 𝑡 e 𝑎 × 𝑡, com foco no significado da reta tangente em cada gráfico. Em seguida, vamos estudar as relações das áreas dos gráficos.

Não podemos confundir o gráfico com a trajetória. A curva de um gráfico é apenas um conjunto de valores definidos por uma relação matemática entre duas variáveis. Por outro lado, a trajetória é o conjunto de posições que são ocupadas pelo móvel.
Navegue pelo conteúdo
Velocidade escalar média
Vamos relembrar a definição matemática de velocidade escalar média:
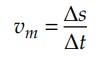
Assim, dado um movimento qualquer de um corpo, não precisamos especificar o seu tipo. Podemos escrever a curva do espaço pelo tempo e, a partir de dois pontos, determinar a velocidade escalar média pelo gráfico:
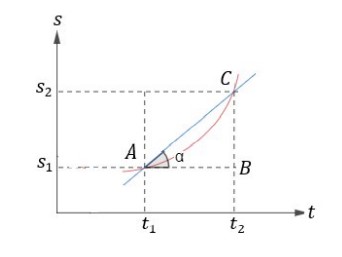
De acordo com o gráfico, podemos calcular 𝑡𝑔𝛼 no triângulo ABC:
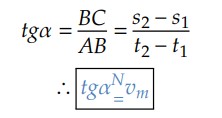
Assim, concluímos que, dado o gráfico do espaço pelo tempo (𝑠 × 𝑡), podemos obter a velocidade escalar média entre dois pontos calculando a tangente do ângulo formado pela reta que liga os pontos e a horizontal, independente de qual seja o tipo do movimento do corpo.
Velocidade escalar instantânea
Para determinarmos a velocidade escalar em um dado instante, temos que usar a definição de velocidade escalar instantânea:
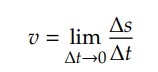
Essa definição mostra que devemos calcular a velocidade escalar média em dois instantes muito próximos. Vamos ilustrar essa operação matemática utilizando o gráfico abaixo:
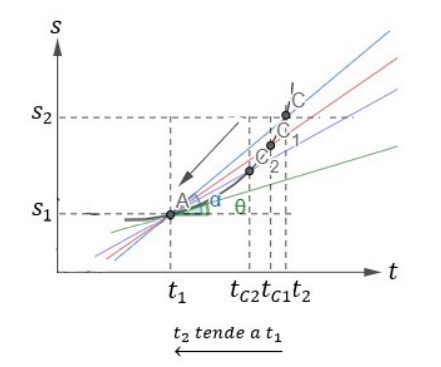
Quando fazemos o Δ𝑡 tender a zero, estamos aproximando 𝑡2 de 𝑡1 – isto é, pegando intervalos de tempo cada vez menores. Assim, a reta secante que une os pontos A e C torna-se a reta tangente no ponto A.
Dessa forma, deixamos de calcular a velocidade escalar média e obtemos a velocidade escalar instantânea no ponto A. Assim, podemos dizer que a velocidade escalar instantânea, em 𝑡1, é numericamente igual à tangente do ângulo que passa por A, isto é:
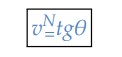
Para o caso do MU, sabemos que a velocidade escalar instantânea é igual à velocidade escalar média, portanto, em qualquer ponto do gráfico de 𝑠 × 𝑡, a reta terá a mesma inclinação, ou seja, o mesmo coeficiente angular. Esse resultado já era esperado, já que no MU a função horária do espaço é dada por:
𝑠 = 𝑠0 + 𝑣.𝑡
Onde 𝑣 é constante.
Aceleração escalar média
Devido às semelhanças nas definições, a análise gráfica da aceleração escalar média é análoga à velocidade escalar média. Atenção! Sempre tome cuidado com os eixos dos gráficos para não confundir e calcular errado.
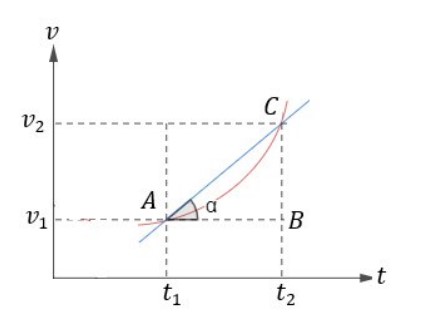
Assim, no gráfico da 𝑣 × 𝑡, podemos calcular a aceleração escalar média entre dois pontos (A e C), por:

Novamente, se desejamos calcular a aceleração escalar média entre dois instantes de um movimento qualquer, é necessário conhecer o valor da tangente do ângulo formado entre a reta que liga os pontos do gráfico – no nosso caso A e C – e o eixo dos tempos.
Aceleração escalar instantânea
Diante das semelhanças nas definições, a análise gráfica da aceleração escalar instantânea segue o mesmo modelo da velocidade escalar instantânea:
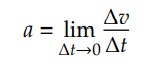
Assim, a aceleração escalar instantânea, em um gráfico 𝑣 × 𝑡, corresponde numericamente à tangente do ângulo entre a reta tangente e o eixo do tempo. Graficamente:
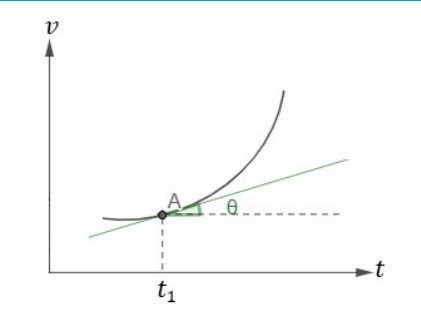
Observação: para simplificar e tornar mais visual a reta tangente, não desenhamos as retas secantes, como feito no gráfico da velocidade escalar instantânea.
Portanto, dizemos que:

Concluímos que para calcular a aceleração escalar instantânea no gráfico 𝑣 × 𝑡, basta acharmos a tangente do ângulo da reta tangente no instante desejado.
No caso do MUV, sabemos que a velocidade escalar é dada por:
𝑣 = 𝑣0 + 𝑎.𝑡
Ou seja, a função horária da velocidade é uma reta. Portanto, tem inclinação constante. Logo, a aceleração escalar instantânea coincide com o coeficiente do gráfico. Sendo assim, a aceleração escalar instantânea é igual à aceleração escalar média, característica desse movimento.
Vimos anteriormente que para calcular a velocidade a partir da função horária do espaço, basta derivarmos a função em relação ao tempo. O mesmo processo é feito para calcular a aceleração a partir da função horária da velocidade.
No Cálculo Diferencial Integral é demonstrado o significado da derivada, que nada mais é do que a reta tangente à função, num dado ponto desejado.
Assim, dado um gráfico de 𝑠 × 𝑡, basta traçarmos a reta tangente num ponto desejado e verificamos como a velocidade se comporta:
a) inclinação para cima: velocidade positiva; e
b) inclinação para baixo: velocidade negativa.
Outro fato importante é a inclinação da reta tangente: quanto mais inclinada a reta tangente, mais cresce a função derivada. Isto é, se tomarmos dois pontos com inclinações diferentes, podemos dizer se uma cresce mais que a outra ou dizer qual inclinação é maior.
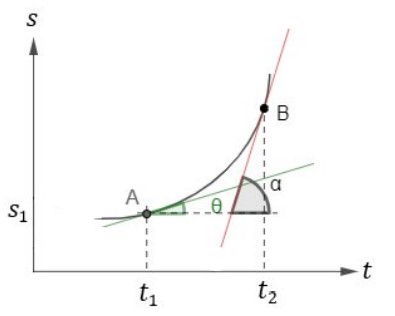
Pelo gráfico, temos que 𝑡𝑔𝛼 > 𝑡𝑔𝛽, logo: 𝑣𝐵 > 𝑣𝐴.
A mesma análise é válida para o gráfico 𝑣 × 𝑡, analisando a aceleração em instantes diferentes.
A partir de agora, vamos estudar qual a representação da área do gráfico com as grandezas físicas da cinemática.
Variação do espaço no gráfico v x t
Vamos utilizar o gráfico do MU para ilustrar o resultado do cálculo da área no gráfico 𝑣 × t.
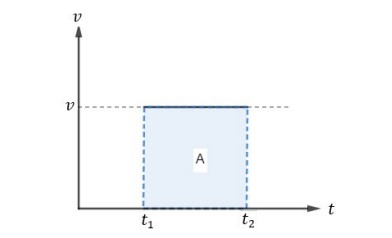
Sabemos que:
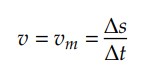
De outra forma: Δ𝑠 = 𝑣.Δ𝑡.
Calculando a área do gráfico de 𝑣 × 𝑡, para o caso do MU, encontramos que:
𝐴 = 𝑣. (𝑡2 − 𝑡1)
Como Δ𝑡 = 𝑡2 − 𝑡1, podemos afirmar que a área é numericamente igual à variação do espaço:
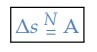
Embora esse seja um caso particular, o resultado é válido para qualquer movimento. Infelizmente, para demonstrar este fato com rigor matemático é necessário recursos do Cálculo Diferencial Integral.
Variação da velocidade escalar no gráfico a x t
De forma análoga aos resultados obtidos para a variação do espaço, vamos mostrar a representação da área no gráfico 𝑎 × 𝑡, especificando para o MUV, em que a aceleração escalar é constante.
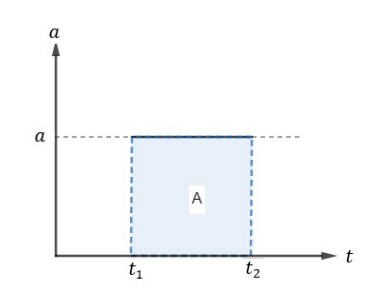
Pela teoria de MUV, sabemos que:
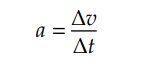
Ou ainda: Δ𝑣 = 𝑎.Δ𝑡.
Quando calculamos a área delimitada pela região azul do gráfico logo acima, concluímos que:
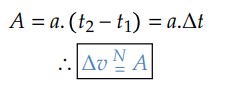
No caso da curva da aceleração não ser constante, serão necessários outros métodos para obtenção da área. Para o caso de a aceleração variar linearmente com o tempo, a velocidade pode ser determinada pela área, com os auxílios da geometria plana.
No caso de outras curvas, apenas com o Cálculo podemos determinar a área embaixo da curva.
Observação: se ao construir o gráfico de 𝑣 × 𝑡 a área estiver abaixo do eixo dos tempos, a variação de espaço é igual a área e coloca-se o sinal negativo.
Contudo, quando se deseja o deslocamento total do móvel, utilizamos os módulos das variações de espaço. Isso é válido para o caso do gráfico de 𝑎 × 𝑡, conforme o exemplo a seguir:
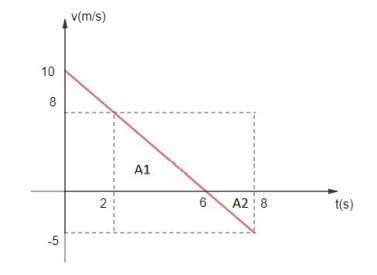
Calcule a variação de espaço e o deslocamento de 2 a 8 segundos.
Para isso, precisamos calcular as áreas de cada intervalo.
Entre 2 e 6 segundos:
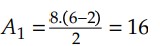
Entre 6 e 8 segundos:
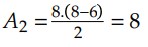
Logo, a variação de espaço do móvel foi de: Δ𝑠 = Δ𝑠1 + Δ𝑠2 = 16 + − 8 = 8 𝑚.
Para determinar o deslocamento, devemos somar os módulos de cada deslocamento:
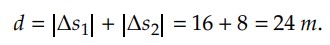
No momento em que o móvel passa pelo eixo dos tempos (no nosso exemplo 𝑡 = 6 𝑠), sua velocidade altera o sentido, isto é, houve inversão no sentido do movimento.
Após esses conceitos iniciais, podemos estudar os gráficos do MUV.
Gráficos no MU
Vamos aos exemplos de gráficos no MU.
Gráfico s x t
Da teoria, sabemos que a função horária do espaço é dada por:
𝑠 = 𝑠0 + 𝑣.𝑡
Trata-se de uma função do primeiro grau, portanto uma reta em que o coeficiente linear é 𝑠0 e o coeficiente angular é 𝑣.
O coeficiente angular é igual a 𝑣. Pela teoria da equação da reta sabemos que o coeficiente angular é igual a tangente do ângulo de inclinação da reta com o eixo horizontal. Portanto, temos que:
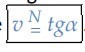
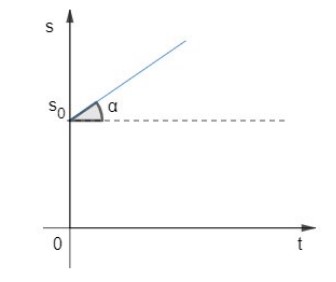
Para 𝑣 > 0, temos o movimento progressivo e a função é crescente, pois o coeficiente angular é positivo, então temos os seguintes gráficos possíveis:
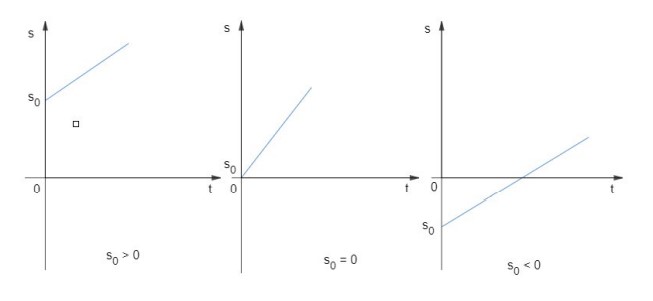
Para 𝑣 < 0 temos o movimento retrógrado, e a função é decrescente, pois o coeficiente angular é negativo. Então, temos os seguintes gráficos possíveis:
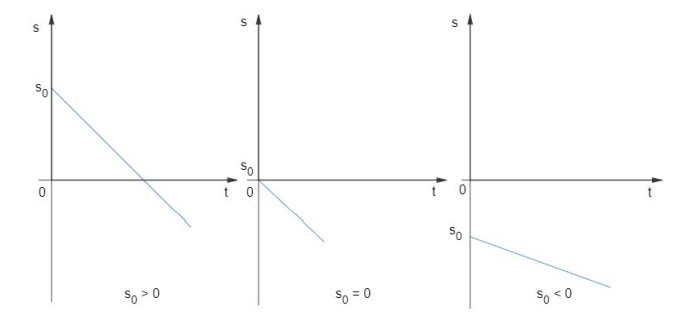
Gráfico v x t
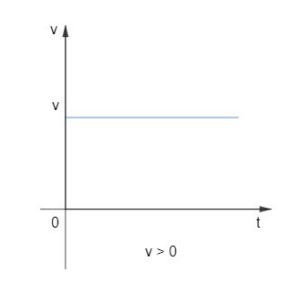
Devido ao fato da velocidade ser constante nesse movimento, temos que o gráfico da velocidade pelo tempo sempre será uma reta paralela ao eixo do tempo.
Para o caso de movimento progressivo, isto é, 𝑣 > 0, a reta paralela está acima do eixo do tempo.
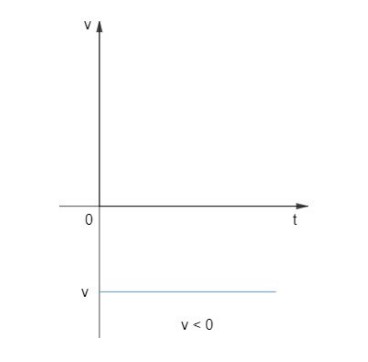
Para o caso de movimento retrógrado, ou seja, 𝑣 < 0, a reta paralela está abaixo do eixo do tempo.
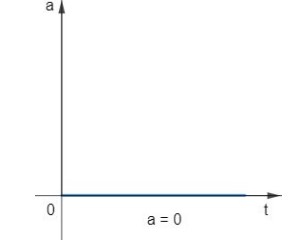
Como a aceleração escalar linear é nula no MU, então a reta da função horária da aceleração é nula, isto é, uma reta que coincidente com o eixo do tempo, independentemente de ser progressivo ou retrógrado.
Gráficos no MUV
Veja os próximos exemplos.
Gráfico s x t
Como visto anteriormente, a função horária do espaço é dada por:
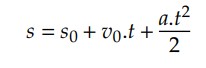
Onde: 𝑎, 𝑣0 𝑒 𝑠0 são constantes.
De acordo com a teoria de função do segundo grau, sabemos que a função 𝑠(𝑡) é uma parábola cuja concavidade depende do valor de 𝑎.
1) Caso 𝒂 > 𝟎:
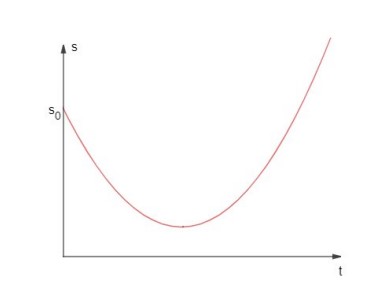
Para ilustrar, tomamos que 𝑠0 > 0 mas o espaço inicial poderia ser menor que zero. Isso não afetaria os resultados teóricos aqui obtidos, apenas estaria deslocada para baixo a curva. No caso de a aceleração escalar positiva, o vértice da parábola representa o espaço mínimo (𝑠𝑉) alcançado pelo móvel no correspondente instante de tempo (𝑡𝑉). Notamos que:
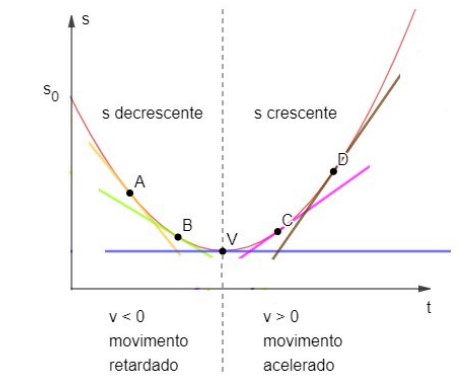
– De 0 a 𝑡𝑉: o espaço do móvel decresce e a inclinação da reta tangente nesse intervalo é negativa, isto é, a velocidade é negativa. Entretanto, 𝑎 > 0 para todo movimento. Como 𝑎.𝑣 < 0, isso implica movimento retardado. Logo, o módulo da velocidade diminui com o tempo.
Quando chegamos no instante 𝑡𝑉, a reta tangente no gráfico neste ponto é horizontal, paralela ao eixo dos tempos. Portanto, a velocidade nesse ponto é nula.
Após este instante, o móvel muda de sentido, seu espaço começa a crescer e a inclinação é positiva. Portanto, temos 𝑣 > 0 e 𝑎 > 0, característica de movimento acelerado.
2) Caso 𝒂 < 𝟎:
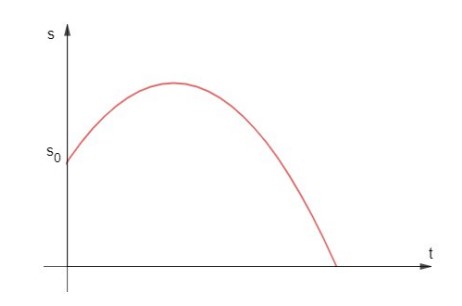
Novamente, pegamos o caso de 𝑠0 > 0, mas os resultados são válidos para qualquer espaço inicial.
Para o caso de 𝑎 < 0, temos que o gráfico acima representa uma parábola com concavidade para baixo, mostrando que o móvel atinge um espaço máximo no vértice da parábola, quando atinge o instante 𝑡𝑉.
Notamos que o espaço é crescente até o instante 𝑡𝑉, isto é, velocidade positiva nesse intervalo de tempo e, como 𝑣 > 0 e 𝑎 < 0, trata-se de um movimento retardado, ou seja, o módulo da velocidade diminui, como visto também pelo fato de a inclinação da reta tangente diminuir a medida que nos aproximamos de 𝑡𝑉.
No instante 𝑡𝑉 a velocidade é nula, característica de mudança de sentido. Para 𝑡 > 𝑡𝑉, o espaço do móvel começa a decrescer, o que significa velocidade negativa. Então, trata-se de um movimento acelerado, pois, 𝑎 < 0 e 𝑣 < 0 (𝑎.𝑣 < 0).
Assim, podemos afirmar que o módulo da velocidade está aumentando, o que também é visto pelo fato da inclinação da reta tangente estar aumentando, em módulo, com o passar do tempo.
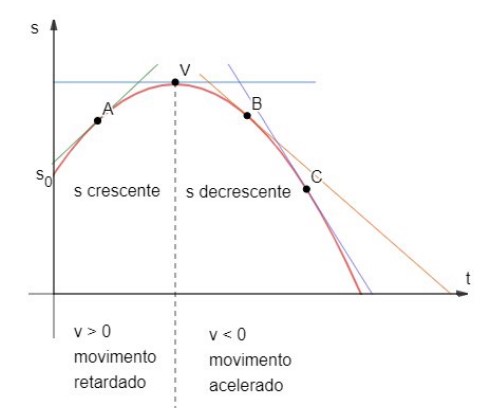
Sendo assim, concluímos que em ambos os casos para 𝑡 < 𝑡𝑉 teremos movimento retardado e para 𝑡 > 𝑡𝑉 teremos movimento acelerado.
Além disso, podemos observar toda vez que a reta tangente é paralela ao eixo dos tempos, a velocidade naquele instante é nula. Isto é válido não só para o MUV, mas para todo movimento variado.
Gráfico v x t
Para o MUV, sabemos que a função horária da velocidade é dada por:
𝑣 = 𝑣0 + 𝑎.𝑡
Com: 𝑣0 e 𝑎 são valores constantes.
Sabemos que essa função é uma reta, onde:
𝑣0: coeficiente linear
𝑎: coeficiente angular
1) Caso 𝒂 > 𝟎:
Trata-se de uma função do primeiro grau crescente, cujo gráfico é dado por:
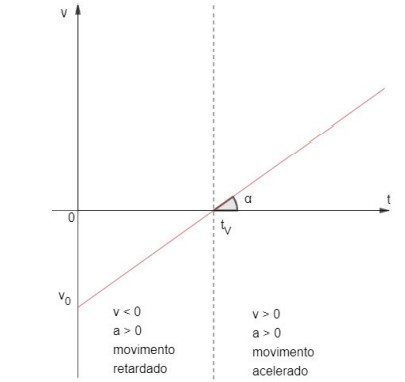
Analisando o gráfico acima, podemos ver que para 0 < 𝑡 < 𝑡𝑉, a velocidade é negativa. Logo, como 𝑎 > 0, trata-se de um movimento retardado, pois temos que 𝑎.𝑣 < 0.
Para 𝑡 = 𝑡𝑉, temos que a velocidade do móvel é nula (mudança de sentido). A partir deste instante, a velocidade é positiva. Logo, como 𝑎 > 0, trata-se de um movimento acelerado, pois temos que 𝑎.𝑣 > 0.
Vale lembrar que a aceleração é numericamente igual a tangente de alfa (𝑎N=𝑡𝑔𝛼).
2) Caso 𝒂 < 𝟎:
Trata-se de uma função do primeiro grau decrescente, cujo gráfico é dado por:
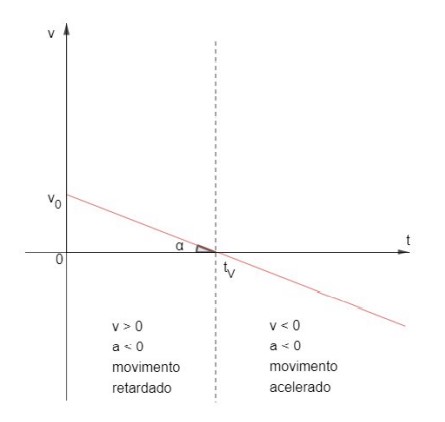
Analisando o gráfico acima, podemos ver que para 0 < 𝑡 < 𝑡𝑉, a velocidade é positiva. Logo, como 𝑎 < 0, trata-se de um movimento retardado, pois temos que 𝑎.𝑣 < 0.
Para 𝑡 = 𝑡𝑉, temos que a velocidade do móvel é nula (mudança de sentido). A partir deste instante, a velocidade é negativa. Logo, como 𝑎 < 0, trata-se de um movimento acelerado, pois temos que 𝑎.𝑣 > 0.
Vale lembrar que a aceleração é numericamente igual a tangente de alfa (𝑎N=𝑡𝑔𝛼).
Neste caso, embora a tangente de alfa seja positiva, a aceleração escalar é negativa, pois trata-se de uma reta decrescente (o cálculo da tangente é apenas para determinação do módulo).
Gráfico a x t
No MUV, sabemos que a aceleração é constante, portanto, existe dois gráficos para a aceleração:
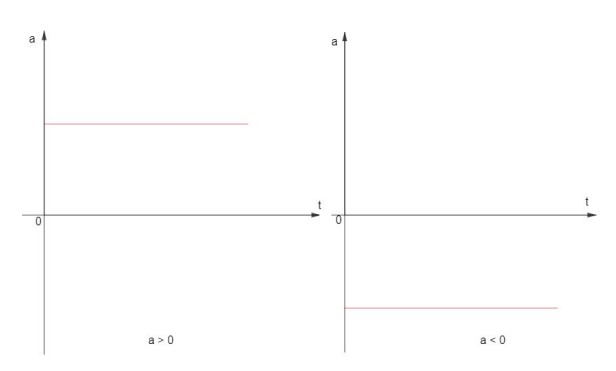
Observação: se a aceleração é nula, então não estamos no MUV, trata-se de um movimento uniforme.
Gostou deste conteúdo? Confira outros temas de Física no portal Estratégia Militares. Aproveite também para conhecer nossos cursos para os Concursos Militares e garanta sua aprovação em 2023!
Veja também:
- Projeções cartográficas: o que são, para que servem, classificação e mais!
- História da Cartografia
- Como é calculado o fuso horário?
- Orientação e localização no planeta
- Saiba como os corpos celestes se movimentam
- Taylorismo, Fordismo e Toyotismo: conheça os modelos de produção
- Comércio mundial e os blocos econômicos: um dos assuntos mais cobrados na sua prova militar
- Massas de ar e suas características: quais são e muito mais
- Floresta equatorial: confira sobre o assunto cobrado nas provas militares
- Hidrografia Brasileira: Bacias Hidrográficas
- Caracterização do Espaço Geográfico
- Problemas Ambientais: entenda o efeito no Brasil
Conteúdo didático elaborado pelo professor Toni Burgatto.



