Depois de todo o conteúdo que o portal Estratégia Militares produziu sobre Movimento Uniforme e Movimento Uniformemente Variado, chegou a hora de estudar o Movimento Circular. Confira a seguir!
Até aqui descrevemos movimentos por intermédio de grandezas escalares lineares, onde elas eram definidas em relação a medidas de comprimentos. A partir de agora, vamos introduzir o conceito de grandeza escalar circular e suas grandezas, como espaço angular, velocidade escalar angular e aceleração escalar angular, tomando como medidas ângulos na circunferência.
Navegue pelo conteúdo
Grandezas angulares
Considere uma partícula realizando o movimento circular da figura.
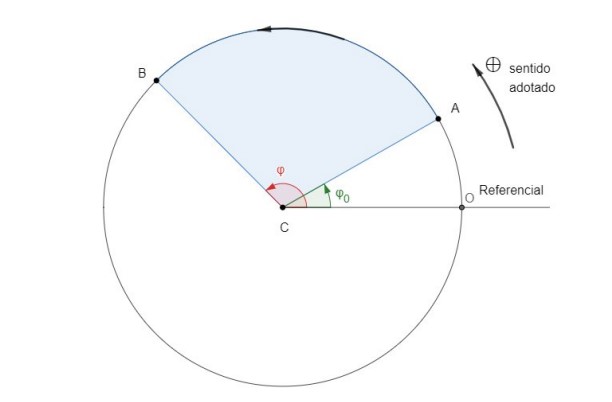
Na figura acima, A é a posição inicial da partícula e B é a posição final da partícula. Aqui, é adotado o sentido anti-horário como positivo. Assim, podemos dizer que:
𝑠0 :𝑒𝑠𝑝𝑎ç𝑜 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
𝑠: 𝑒𝑠𝑝𝑎ç𝑜 𝑓𝑖𝑛𝑎𝑙
Devido à trajetória ser circular, podemos escrever a posição inicial e final do ponto material utilizando ângulos:
𝜑0 : 𝑒𝑠𝑝𝑎ç𝑜 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
𝜑: 𝑒𝑠𝑝𝑎ç𝑜 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑓𝑖𝑛𝑎𝑙
Vale lembrar a relação da geometria plana para ângulos em radianos:
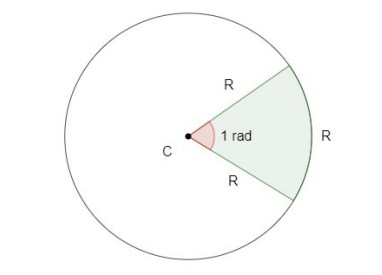
Então, estabelecemos uma relação entre o ângulo central e o comprimento do arco de circunferência:

Logo:
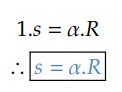
Atenção: ângulo 𝛼 em radianos.
Além disso, como a definição de radianos envolve a divisão entre duas grandezas de distâncias, os radianos tornam-se essencialmente adimensionais.
Assim, podemos escrever a variação angular da partícula, como:
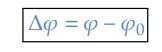
Dessa forma, define-se velocidade angular média como a razão entre a variação do espaço angular e a variação do tempo correspondente:

Analogamente à velocidade escalar, define-se velocidade angular instantânea como o limite da velocidade angular média para Δ𝑡 tendendo a zero:
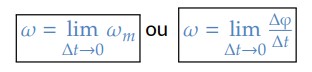
Portanto, a velocidade angular instantânea é a derivada do espaço angular em relação ao tempo:
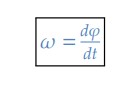
Como os espaços angulares são expressos em radianos e o tempo em segundos, a unidade de velocidade angular é expressa em radianos por segundo (rad/s).
Semelhante a definição de aceleração escalar média, define-se aceleração angular média como a razão entre a variação da velocidade angular e o intervalo de tempo correspondente:

Como a velocidade angular é expressa em rad/s e o tempo em segundos, a unidade de aceleração angular é rad/s².
A aceleração angular instantânea é definida pelo limite da aceleração angular média quanto Δ𝑡 tende a zero:
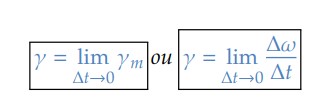
Portanto, a aceleração angular instantânea é a derivada da velocidade angular em relação ao tempo:
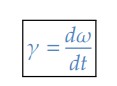
Pela geometria plana, podemos escrever algumas relações entre as grandezas escalares lineares e as grandezas angulares:
- Relação de ângulo com comprimento de arcos na circunferência:
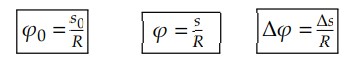
- Relação entre velocidade linear média e velocidade angular média:
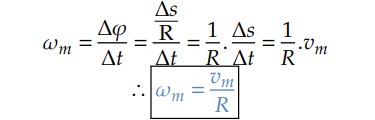
Para velocidades instantâneas, também vale a relação:

- Relação entre aceleração linear média e aceleração angular média
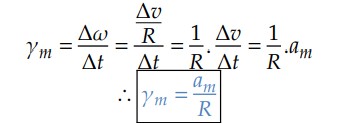
Para acelerações instantâneas, também vale a relação:
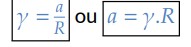
Gostou desse conteúdo sobre Movimento Circular? Continue acompanhando os posts com conteúdo de Física no portal Estratégia Militares e se prepare para os concursos militares! Clique no banner abaixo e conheça nossos cursos!
Veja também:
- Projeções cartográficas: o que são, para que servem, classificação e mais!
- História da Cartografia
- Como é calculado o fuso horário?
- Orientação e localização no planeta
- Saiba como os corpos celestes se movimentam
- Taylorismo, Fordismo e Toyotismo: conheça os modelos de produção
- Comércio mundial e os blocos econômicos: um dos assuntos mais cobrados na sua prova militar
- Massas de ar e suas características: quais são e muito mais
- Floresta equatorial: confira sobre o assunto cobrado nas provas militares
- Hidrografia Brasileira: Bacias Hidrográficas
- Caracterização do Espaço Geográfico
- Problemas Ambientais: entenda o efeito no Brasil
Conteúdo didático elaborado pelo professor Toni Burgatto.



