Preparado para mais um conteúdo sobre Física do Portal Estratégia Militares? Desta vez, vamos dar continuidade aos estudos dos Movimentos Circulares. Quer saber como se dá a transmissão destes movimentos e como calculá-los? Confira nosso novo conteúdo!
Navegue pelo conteúdo
Correia comum a duas rodas ou por contato direto
É comum utilizar a transmissão de movimentos para fins de amplificar ou reduzir uma
grandeza física. O exemplo mais comum está em uma bicicleta, na qual o ciclista estabelece uma velocidade na correia dos pedais, que é transmitida por uma corrente para a correia da roda de trás.
Podemos representar essa transmissão pela figura abaixo:
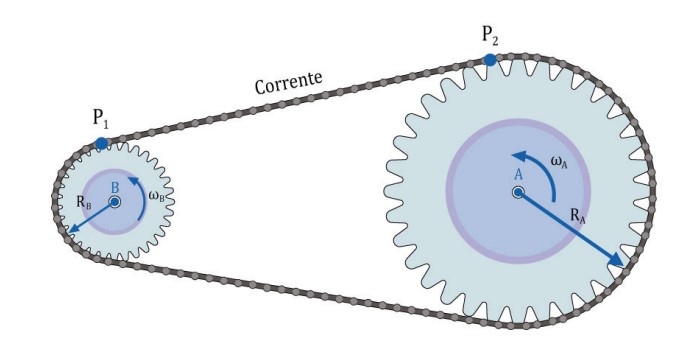
Se não existir escorregamento entre a corrente e as coroas, podemos dizer que a velocidade linear das duas coroas é igual a velocidade da corrente. Ou seja: a velocidade linear é a mesma em qualquer ponto da corrente. Portanto:
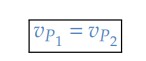
Desta forma, podemos encontrar uma relação para as velocidades angulares e as frequências para este conjunto:
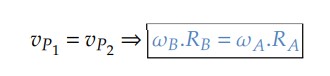
Como 𝜔 = 2𝜋𝑓, então:
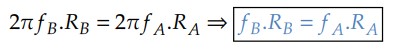
Assim, podemos concluir que se 𝑅𝐴 > 𝑅𝐵, então 𝜔𝐴 < 𝜔𝐵 e 𝑓𝐴 < 𝑓𝐵.
De forma análoga, podemos chegar às mesmas conclusões para o caso das coroas – ou engrenagens – em contato direto:
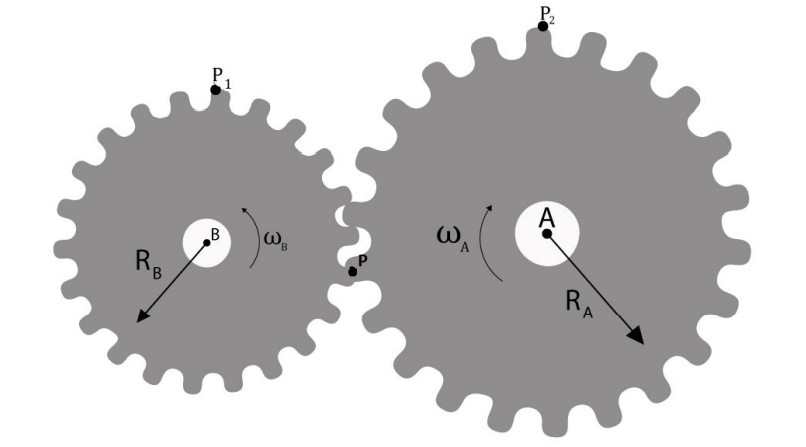
Como as duas engrenagens se encontram em um ponto em comum, suas velocidades lineares devem ser as mesmas, desde que não haja escorregamentos:
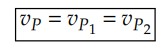
Então:
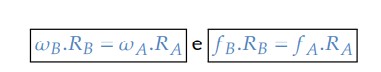
Novamente, podemos concluir que se 𝑅𝐴 > 𝑅𝐵, então: 𝜔𝐴 < 𝜔𝐵 e 𝑓𝐴 < 𝑓𝐵.
Caso o móvel esteja realizando um Movimento Circular Uniformemente Variado (MCUV), a conclusão é a seguinte:
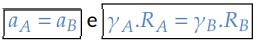
Engrenagens com mesmo eixo de rotação
Vamos considerar a transmissão entre as duas engrenagens ligadas por um mesmo eixo, como na figura a seguir:
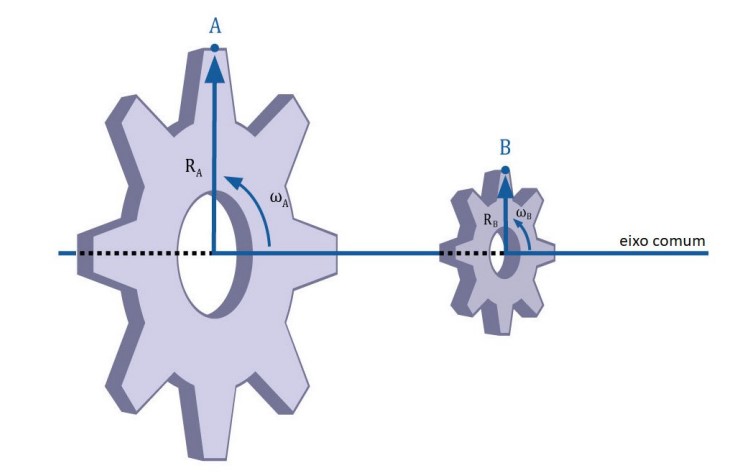
Neste caso, podemos ver que se pegarmos um ponto na coroa B, sua projeção na coroa A terá a mesma variação angular. Dessa forma, podemos deduzir que:
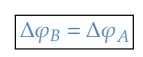
Assim, as velocidades angulares e as frequências serão as mesmas:
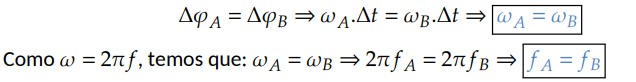
Para velocidades lineares, encontramos que:
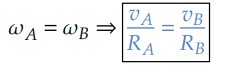
Concluímos que se 𝑅𝐴 > 𝑅𝐵, então: 𝑣𝐴 > 𝑣𝐵.
Caso o móvel esteja realizando um MCUV, a conclusão será a seguinte:
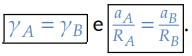
Até aqui, deduzimos todas as equações para o caso de transmissão no MCU. Entretanto, toda análise feita é válida para qualquer tipo de movimento circular.
Gostou de mais este tema de Física? Leia outros posts com conteúdos didáticos no Portal Estratégia Militares. E se você deseja entrar para as Forças Armadas, conheça os nossos cursos preparatórios. Clique no banner abaixo e saiba mais!
Veja também:
- Operações matemáticas com algarismos significativos
- Noções de Algarismos Significativos
- Cinemática Escalar: introdução
- Cinemática Escalar: velocidade escalar média, movimento progressivo e mais
- Física: introdução, grandeza, estudo e mais
- Movimento uniformemente variado: aceleração, cinemática com cálculo e mais!
- Movimento uniforme: o que é e para que serve?
Conteúdo didático elaborado pelo professor Toni Burgatto.



