O movimento uniforme é um conteúdo de Física que está sempre presente em questões de concursos de qualquer tipo. Por isso, o portal Estratégia Militares traz até você um artigo sobre o tema. Confira!
Navegue pelo conteúdo
O que é movimento uniforme?

Caracteriza-se como movimento uniforme aquele que possui velocidade de módulo constante e diferente de zero, isto é:
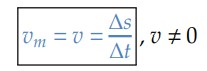
Ou, também podemos dizer que: Δ𝑠 = 𝑣.Δ𝑡.
Escrevendo dessa forma, vemos que a variação do espaço (Δ𝑠) é diretamente proporcional ao intervalo de tempo correspondente (Δ𝑡).
Além disso, vemos que Δ𝑠 varia linearmente com Δ𝑡. Portanto, para intervalos de tempos iguais, as variações de espaços também são iguais, como mostra a figura abaixo:

Quando o movimento uniforme for em uma reta, chamamos de Movimento Retilíneo Uniforme (MRU). Quando for em uma circunferência, chamamos de Movimento Circular Uniforme (MCU).
Lembrete: velocidade é uma grandeza vetorial!
Função horária do espaço
Definido o espaço inicial como s0 correspondente ao instante 𝑡0, para um instante 𝑡 temos que o espaço será 𝑠, com Δ𝑡 = 𝑡 − 𝑡0 e Δ𝑠 = 𝑠 − 𝑠0.A partir de Δ𝑠 = 𝑣.Δ𝑡, concluímos que:
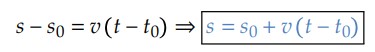
Geralmente, adotamos como tempo inicial 𝑡0 = 0, quando zeramos cronômetro e passamos a contar o tempo a partir do zero. Dessa forma, a função do espaço para o MRU se reduz a:
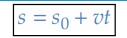
Isto é, a função horária do espaço é uma função do primeiro grau em 𝑡.
A principal característica do movimento retilíneo uniforme é o fato da velocidade escalar ser constante, isto é, a aceleração escalar é nula.
Para verificar se um movimento é MU, devemos observar se o movimento respeita qualquer uma destas três características:
1) A velocidade escalar instantânea é constante:
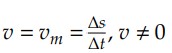
2) O espaço obedece a uma função horária do primeiro grau em 𝑡: 𝑠 = 𝑠0 + 𝑣𝑡
3) A aceleração escalar instantânea é nula: 𝑎 = 𝑎𝑚 = 0
Gráficos no MU
Dado que a função horária do espaço é dada por 𝑠 = 𝑠0 + 𝑣𝑡, então a função de 𝑠(𝑡) é uma função do primeiro grau, análoga a 𝑓 (𝑥) = 𝑏 + 𝑎𝑥. Então, dada a 𝑠(𝑡) = 𝑠0 + 𝑣𝑡, temos que 𝑠0 é o coeficiente linear da função e 𝑣 é o coeficiente angular da função.
Na matemática, lembramos que o coeficiente linear caracteriza o ponto onde a função toca quando passa pelo eixo y. Já o coeficiente angular nos mostra a inclinação da reta, isto é, a taxa como cresce ou descreve a função.
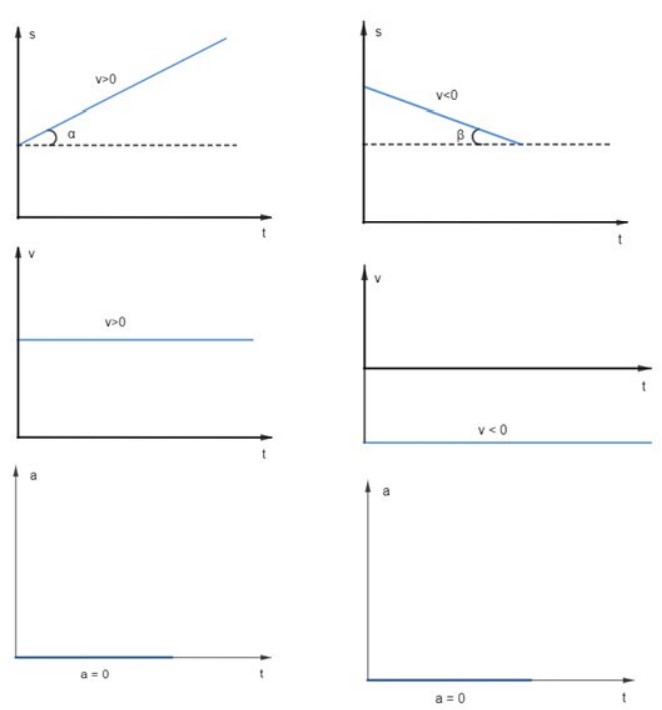
Diagrama s X t
No movimento progressivo (𝑣 > 0), o espaço cresce (Δ𝑠 > 0) com o tempo (figura 2) e, no movimento retrógrado (𝑣 < 0), o espaço decresce (Δ𝑠 < 0) com o tempo (figura 3).
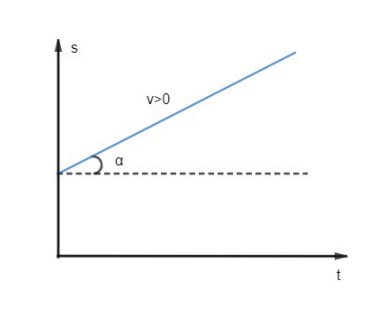
Dado que:
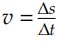
E que, segundo a trigonometria, tangente é uma função que é definida pela razão do cateto oposto pelo cateto adjacente, temos que:
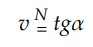
Isto é, a tangente da inclinação da reta é igual numericamente à velocidade.
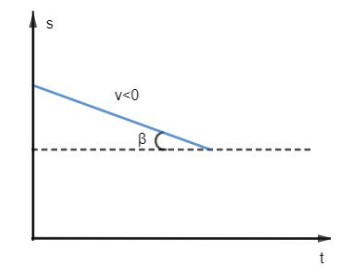
Para o caso do movimento retrógrado, a 𝑡𝑔𝛽𝑁= |𝑣|. Entretanto, temos que nesse caso a velocidade é negativa, então, devemos lembrar de colocar o sinal de menos após calcular a tangente para de fato determinar a velocidade.
Diagrama 𝒗 × t
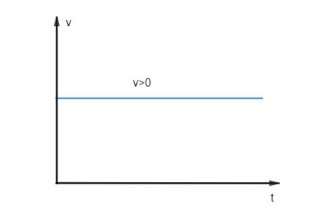
O MU é caracterizado por ter velocidade constante, dessa forma, o módulo da velocidade não se altera com o decorrer do tempo. Logo, a função da velocidade com o tempo é uma reta paralela ao eixo dos tempos. Para o movimento progressivo temos 𝑣 > 0, logo, a reta é paralela e está acima do eixo dos tempos.
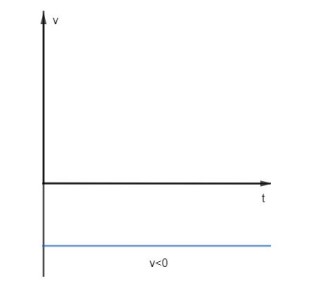
Para o movimento retrógrado temos 𝑣 < 0, portanto, a reta é paralela e está abaixo do eixo dos tempos, conforme as figuras abaixo:
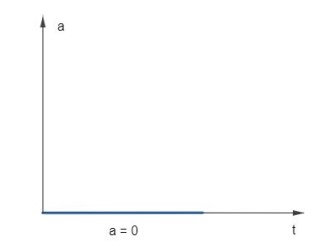
Como dito anteriormente, neste movimento não existe aceleração, logo o gráfico da aceleração pelo tempo coincide com o eixo dos tempos.

Gostou desse conteúdo? Leia outras matérias sobre Física aqui no portal e saia na frente em seus estudos.
Se quiser uma preparação que é líder no que vale: classificação, conheça os cursos do Estratégia Militares. Clique no banner e saiba mais!
Veja também:
- Operações matemáticas com algarismos significativos
- Noções de Algarismos Significativos
- Cinemática Escalar: introdução
- Cinemática Escalar: velocidade escalar média, movimento progressivo e mais
- Física: introdução, grandeza, estudo e mais
- Movimento uniformemente variado: aceleração, cinemática com cálculo e mais!
Conteúdo didático elaborado pelo professor Toni Burgatto.



