Os conteúdos de física são fundamentais para muitos Concursos Militares. Por isso, confira esta nova publicação do portal Estratégia Militares e saiba mais sobre vetores!
Navegue pelo conteúdo
Introdução
Podemos dividir as grandezas físicas em escalares e vetoriais. As escalares necessitam apenas da sua magnitude e sua unidade de medida para estarem definidas. Por outro lado, as grandezas vetoriais precisam de mais informações.
Vamos usar o exemplo de quando estamos perdidos e pedimos informações para alguém. Se a pessoa disser apenas que você está a alguns quilômetros do seu destino, isso não é suficiente para chegar até lá. As perguntas que você fará para o informante é: para qual direção? E qual sentido?
O estudo dos vetores é fundamental para a melhor compreensão das grandezas físicas. Algumas definições são feitas diretamente por produto escalar ou produto vetorial, por exemplo. Por isso, vamos estudar o que são vetores e os principais cálculos utilizados na Física.
Definições básicas dos vetores
Vetor é um ente matemático determinado por segmentos orientados, caracterizados por: módulo, direção e sentido.
Para representá-lo no espaço, precisamos definir um comprimento proporcional ao seu módulo, sempre um número real positivo.
Normalmente, indicamos um vetor por uma letra com uma flecha em cima. Em textos impressos, os vetores podem ser denotados também por negrito: ?,?,?,? , etc. Para se referir apenas ao módulo do vetor, representamos como mostrado na figura abaixo:
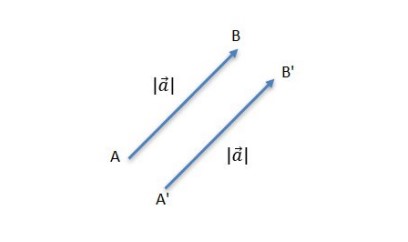
Assim, verificamos que os segmentos ?? e ?′?′ estão em direções orientadas paralelas entre si, com mesmo sentido, e os comprimentos destes segmentos de retas são iguais. Diante disso, podemos afirmar a condição de igualdade entre dois vetores:
Dois vetores são iguais entre si quando possuem o mesmo módulo, a mesma direção e o mesmo sentido.
Assim, podemos dizer que: ?? = ?′?′ = ?. Portanto, ? é o vetor que os dois segmentos de reta representam.
Operações matemáticas com vetores
Semelhante à álgebra dos números, é possível realizar diversas operações com vetores. Vamos citar as mais usuais em física. Para realizar essas operações é necessário tomar alguns cuidados, pois, diferente dos números, existem regras próprias.
Algumas operações com vetores:
- Adição de vetores;
- Multiplicação de vetor por escalar;
- Subtração de vetores;
- Produto escalar; e
- Produto vetorial.
Adição de vetores
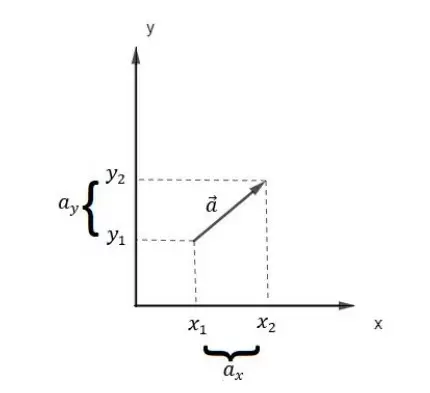
Para somar dois vetores, vamos introduzir a ideia por meio de um exemplo. Suponha que um jovem atleta deseje correr em uma praça em formato de um triângulo retângulo conforme a figura abaixo. Ele sai do ponto A em direção ao ponto B, em seguida para o ponto C.
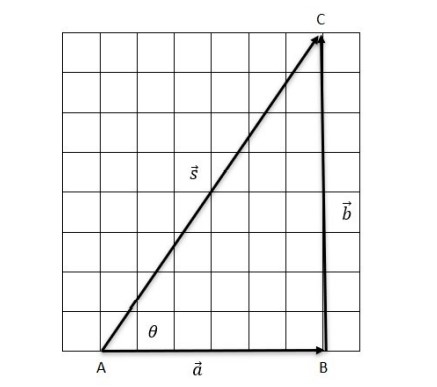
A praça possui as seguintes dimensões: ?? = 60 ?, ?? = 80 ? e ?? = 100 ?. Indicamos por ? o vetor deslocamento no trecho ??, por ? o vetor deslocamento no trecho ?? e por ? o deslocamento resultante. Matematicamente, dizemos que:
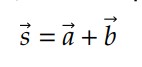
Observe que, em módulos, ? ≠ ? + ?, isto é, o tamanho do vetor ? é diferente da soma dos módulos de ? e ?. Para encontrar o módulo do vetor resultante, dados que ? e ? são perpendiculares entre si, utilizaremos sempre o teorema de Pitágoras:
? 2 = ?2 + ?2
? 2 = 602 + 802
? = 100 ?
Até aqui, foi definido apenas o módulo do vetor ?. Para definir completamente o vetor, precisamos definir a direção, isto é, o ângulo ? que o vetor faz com o segmento ??. Este ângulo pode ser determinado por intermédio da tangente do ângulo ?:
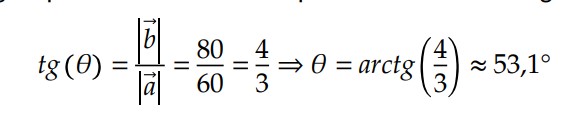
A partir desse exemplo, podemos ver que somar dois vetores não é simplesmente somar dois números. Somar vetores é uma operação geométrica.
Antes de caminharmos para as regras de adição de vetores, vamos trabalhar alguns casos especiais, onde os vetores estão na mesma direção.
Vetores com mesma direção e mesmo sentido
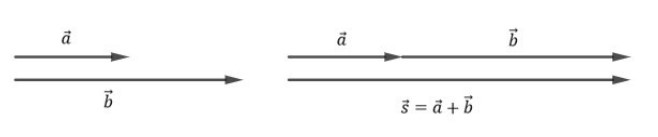
Dessa forma, ao somar dois vetores que têm a mesma direção e mesmo sentido, o vetor resultante terá a mesma direção e sentido dos operandos e seu módulo será a soma dos módulos.
Vetores com mesma direção e sentidos opostos
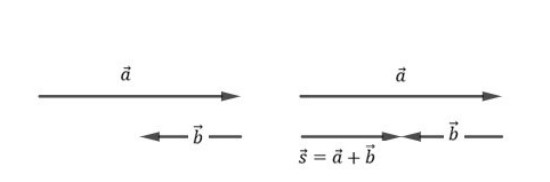
Ao somarmos dois vetores que têm mesma direção e sentidos opostos, a direção do vetor resultante será a mesma dos vetores operandos, mas o sentido será mesmo determinado por aquele que tiver o maior módulo. O módulo do vetor resultante será dado pela diferença do maior módulo com o menor módulo.
Existem três métodos para somar vetores: regra do paralelogramo, regra do polígono e a decomposição de vetores. Neste primeiro artigo, iremos ver apenas as duas primeiras.
Regra do Paralelogramo
Este método é utilizado para calcular a soma de dois vetores quando é conhecido o ângulo formado entre eles. Geralmente, quando usamos esse método, utilizamos a lei dos cossenos para a determinação do vetor resultante.
Vamos recordar duas leis importantes da geometria plana para um triângulo qualquer:
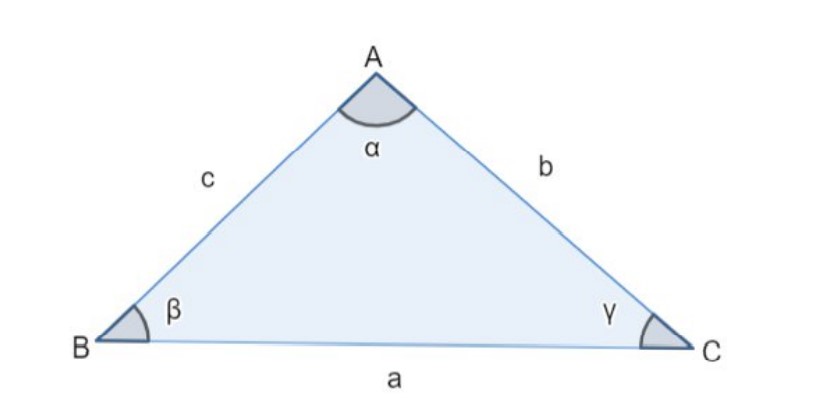

Depois de relembrar essas duas leis, vamos aplicá-las na regra do paralelogramo.
Primeiramente, colocamos os dois vetores com origem em comum (ponto O) e construímos um paralelogramo, fazendo linhas tracejadas paralelas aos vetores, passando pelas extremidades dos operandos.
Em seguida, liga-se a origem dos vetores (ponto O) ao encontro das linhas tracejadas (ponto C), determinando o vetor resultante
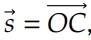
conforme figura abaixo:
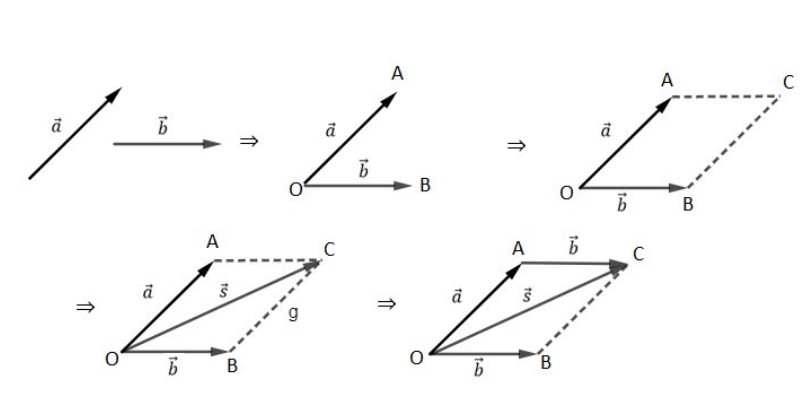
Olhando para o paralelogramo abaixo, podemos aplicar a regra do paralelogramo, lembrando algumas propriedades da Geometria Plana e da Trigonometria:
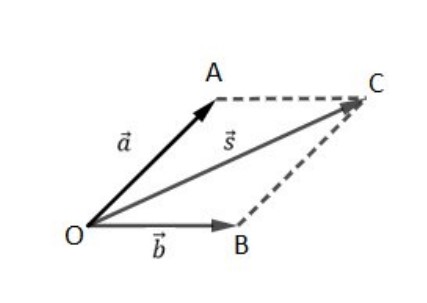
No triângulo AOC, vamos chamar o ângulo ?Â? de ? e o ângulo ?Ô? de ? (ângulo entre os dois vetores). De acordo com a Geometria Plana, ? + ? = 180° ⇒ ? = 180 − ?. Da Trigonometria, sabemos que cos ? =− ????. Então, aplicando a lei dos cossenos para o triângulo AOC, temos:
? 2 = ?2 + ?2 − 2?.?. cos ? ⇒ ?2 = ?2 + ?2 + 2.?.?. − ???? ⇒
?2 = ?2 + ?2 + 2.?.?.????
Diante desse resultado, podemos criar um método para determinar o módulo do vetor soma. Aplicando os passos:
1) Coloca-se os vetores em origem comum;
2) Conhecemos o valor do ângulo formado pelos vetores que queremos somar;
3) Cumpridos os passos 1 e 2, aplicamos a fórmula anterior e encontramos o vetor desejado.
Esse método limita-se à soma de dois vetores apenas. Para somar mais vetores, precisamos aplicar a regra do paralelogramo para dois vetores e, a partir do resultante, aplicar novamente a regra – e assim sucessivamente.
Isso torna o método nada usual para o caso da soma de n vetores. Então, veremos uma regra mais útil para esse tipo de problema: a regra do polígono.
Regra do Polígono
Vamos pegar quatro vetores distintos, de acordo com a figura abaixo:
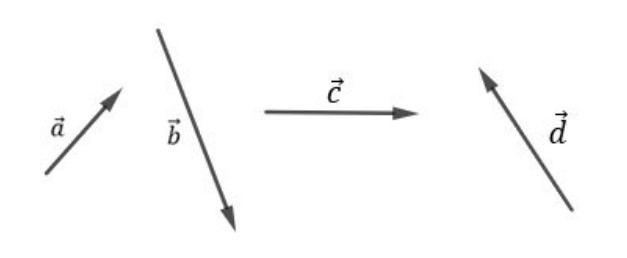
O vetor resultante pode ser obtido da seguinte forma:
1) Escolha um vetor para ser o “vetor origem” (escolhemos o vetor ?). A partir dele, escolha qualquer um (escolhemos o vetor ?) e coloque a origem do vetor escolhido na extremidade do “vetor origem”;
2) Em seguida, escolha qualquer um dos vetores que sobrou e coloque a origem na extremidade do vetor anterior (?) e assim, até que todos os vetores estejam colocados em ordem, a origem na extremidade do anterior;
3) O vetor resultante está determinado ligando a origem do primeiro vetor à extremidade do último.
A figura abaixo ilustra nosso exemplo:
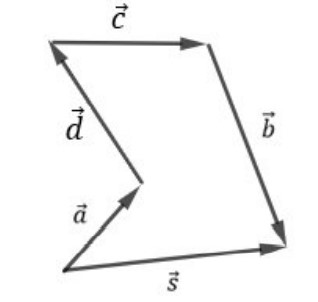
A forma como mostramos a regra do polígono ilustra as propriedades comutativa e associativa da soma de vetores.

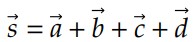
e pelas propriedades comutativa e associativa podemos escrever que:
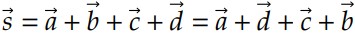
Com esse exemplo, vemos que não importa a ordem como escolhemos os vetores, desde que sejam respeitadas as regras.
Além disso, podemos ver que se efetuarmos a soma e a extremidade do último cair na origem do primeiro, teremos um polígono fechado dos vetores, de tal forma que a extremidade do vetor soma coincide com a própria origem. Então, o vetor resultante será o vetor nulo (0).
Decomposição de Vetores
Este método é muito importante na Física, já que podemos descrever diversas grandezas vetoriais em sistemas de coordenadas 𝑥𝑦𝑧, na resolução de problemas com três dimensões, ou em sistema 𝑥𝑦, em duas. É comum colocar as variáveis em um mesmo eixo para solucioná-las.
Vamos pegar um vetor 𝐹 qualquer, que pode ser uma força, por exemplo. Pela regra do paralelogramo, estudada no conteúdo anterior, podemos dizer que ele é a soma de outros dois vetores, por exemplo:
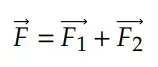
Assim, é interessante observar que, para fazer os cálculos, deve-se escolher um paralelogramo que possua propriedades que facilitem nossas contas.
Na matemática sabemos que um retângulo é um tipo de paralelogramo com ângulos de 90° e o que facilita muito os cálculos. Então, o melhor caminho é escolher vetores que sejam ortogonais, isto é, formam um ângulo de 90° quando colocadas as origens em comum.
Uma vez que os vetores podem ser ortogonais, podemos usar os sistemas de eixos coordenadas para auxiliar.
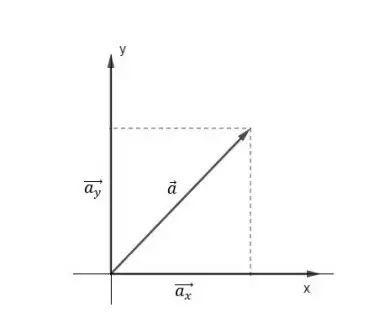
Dessa forma, podemos escrever 𝐹 como a soma de um vetor no eixo x (𝐹𝑥 ) e outro vetor no eixo y (𝐹𝑦 ). Assim, temos que:
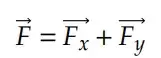
Podemos representar da seguinte forma:
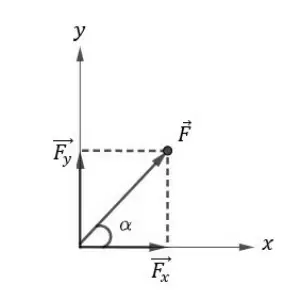
Esses vetores 𝐹𝑥 e 𝐹𝑦 são chamados de projeções do vetor 𝐹 nos eixos 𝑥 e 𝑦, respectivamente. Pela geometria, podemos dizer que:
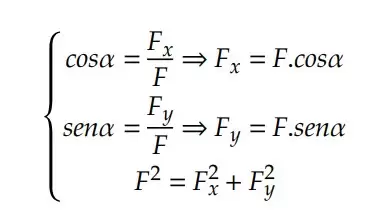
Por esse método, se temos vários vetores a serem somados, basta colocar todos na mesma origem e os projetar nos eixos 𝑥 e 𝑦. Em seguida, efetua-se a soma de acordo com as regras de adição em mesma direção, obtendo um vetor resultante em cada eixo.
Para concluir, basta usar a regra do paralelogramo para esses dois vetores restantes para obter o vetor soma desejado. Como os eixos são sempre ortogonais, vamos sempre recair em dois vetores ortogonais, com fácil aplicação do teorema de Pitágoras para o vetor desejado.
Exemplo: determine o vetor soma 𝑠 entre os vetores dados 𝑎, 𝑏, 𝑐. Dado que cos 𝛼 = 0,6 e 𝑠𝑒𝑛𝛽 = 0,8.
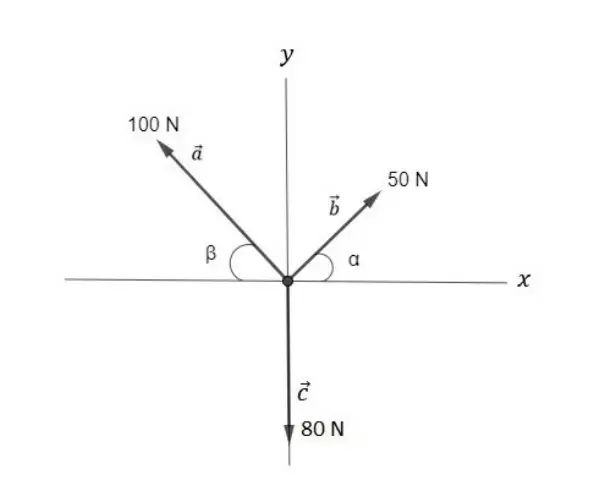
Primeiramente, iremos decompor cada vetor nos eixos x e y:
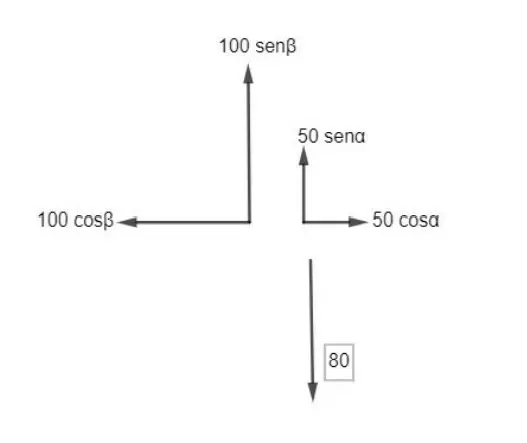
Assim, temos que:
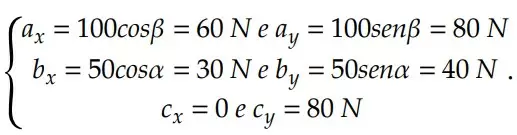
Portanto, temos os seguintes vetores resultantes para cada eixo:
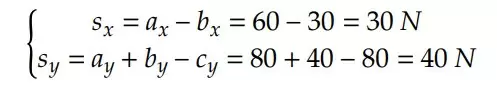
Assim, reduzimos nossos vetores aos resultantes em cada eixo:
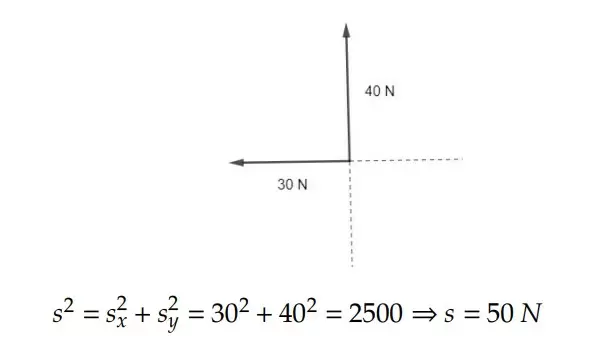
Para finalizar, devemos determinar sua direção e sentido para que o vetor fique completamente definido, como na figura abaixo:
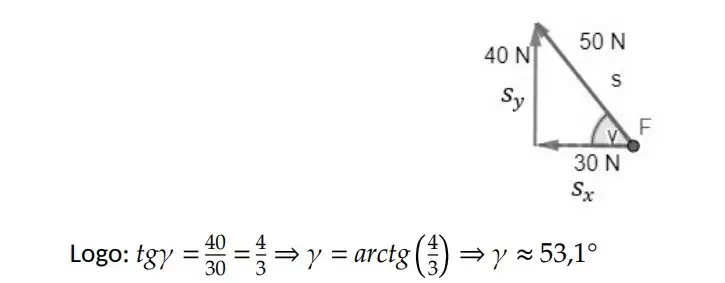
Com esse exemplo, concluímos que qualquer vetor pode ser projetado em eixos ortogonais entre si. Dado um sistema coordenado no 𝑅3 (𝑥,𝑦,𝑧), conforme figura abaixo, podemos decompor o vetor 𝑎 nos três eixos:
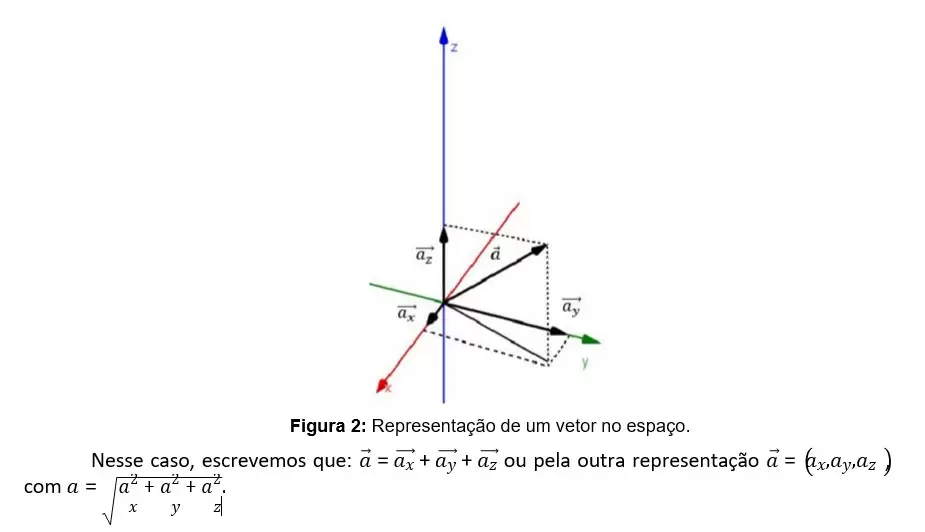
Assim, representar um vetor por suas componentes torna a operação de soma muito mais simplificada, pois, para somar dois vetores, basta somar as partes:
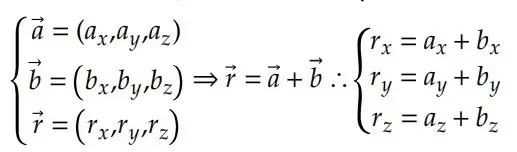
Multiplicação por um escalar
Outra operação muito comum e importante no universo dos vetores é a multiplicação de um vetor por um escalar. Podemos anotar essa operação da seguinte forma:
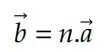
Onde 𝑛 é um número real qualquer, 𝑏 é o vetor obtido ao multiplicar o vetor 𝑎 pelo escalar 𝑛.
Como resultado dessa definição, podemos notar que:
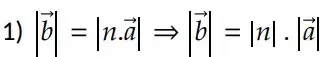
Isto é, o módulo do vetor obtido é o produto do módulo do escalar pelo módulo do vetor multiplicado.
Multiplicar pelo escalar é alterar o tamanho do vetor. Ao efetuar essa operação existem dois possíveis tipos de mudança no módulo:
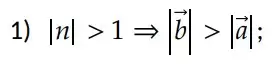
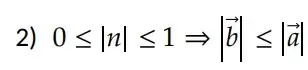
2) 𝑏 tem a mesma direção de 𝑎;
3) o sentido de 𝑏 é o mesmo de 𝑎 quando 𝑛 > 0 e o sentido de 𝑏 é o contrário de 𝑎 quando 𝑛 < 0. Se 𝑛 = 0, obtemos como resultado o vetor nulo, representado por 0.
Quando o vetor representado na forma 𝑎 = (𝑎𝑥 ,𝑎𝑦 ,𝑎𝑧), então o valor de 𝑏 = 𝑛.𝑎 é dado por 𝑏 = (𝑛𝑎𝑥 , 𝑛𝑎𝑦 , 𝑛𝑎𝑧);
4) Para o caso de 𝑛 = − 1, o vetor obtido recebe o nome de vetor oposto, pois como para os números, o oposto é um número que somado ao próprio número dá como resultado zero.
Por exemplo, o oposto de 10 é -10, pois 10 + − 10 = 0. Como visto no item anterior, ao multiplicar por um número negativo, troca-se o sentido do vetor. Dessa forma, o vetor oposto a 𝑏 é o vetor − 𝑏, pois, teremos que:
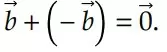
Neste momento, podemos falar de um vetor muito importante para representações físicas, com uma aplicação que facilita muito nossa vida.

Vetores unitários
Vetor unitário – chamado, às vezes, de versor – é aquele cujo módulo é igual a 1.
Existem dois vetores unitários que formam a base canônica, no 𝑅2 ((𝑥,𝑦)), que são dados por:
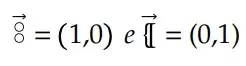
Para o 𝑅3, temos a seguinte base canônica:
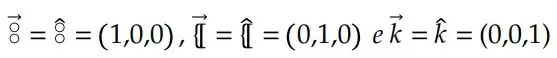
Para construir um vetor unitário 𝑢 que tenha a mesma direção e o mesmo sentido que o vetor 𝑎, devemos dividir o vetor 𝑎 pelo seu módulo:
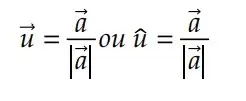
Decomposição de vetores em vetores unitários
Para facilitar nossas contas, podemos decompor os vetores em vetores unitários em cada um dos planos apresentados. Vamos fazer para o ℝ2, mas para o ℝ3 ocorre de forma análoga. Tomemos um vetor no ℝ2:
Por convenção, simbolizamos os vetores unitários com um “chapéu”:
Dessa forma, podemos dizer que:
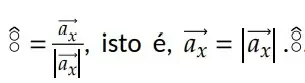
Então, podemos escrever a projeção em um eixo como sendo o produto do vetor unitário daquele eixo pelo módulo da projeção. Assim, temos que:
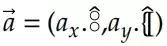
Caso o vetor 𝑎 estivesse sendo trabalhado no 𝑅3, teríamos que:
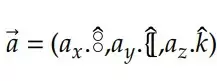
Caso o vetor não esteja na origem, podemos escrevê-lo da seguinte forma:
Assim, podemos escrever o vetor da seguinte forma:
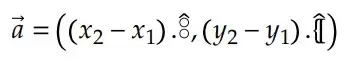
Subtração de vetores
Para efetuar a subtração de vetores, basta pensarmos que a subtração é um caso particular da adição, devido à existência do elemento oposto. Assim, podemos fazer:
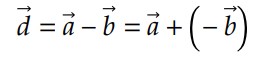
Em outras palavras, para fazer a subtração basta somar o primeiro com o oposto do segundo. Geometricamente podemos ver a operação:
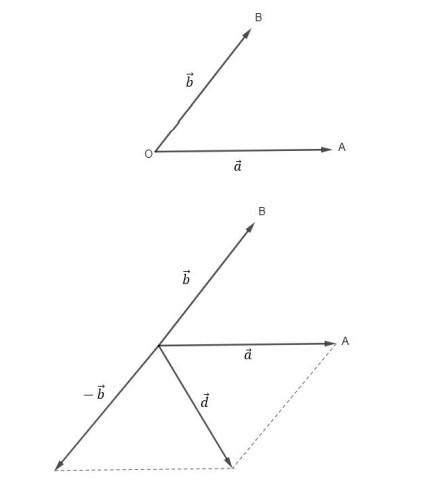
Analisando a figura acima, podemos criar um método para efetuar a subtração geometricamente.
Inicialmente, colocamos os dois vetores em origem comum e traçamos o vetor diferença ligando a extremidade do segundo termo da subtração (𝑏) à extremidade do primeiro termo (𝑎), sempre nessa ordem, como indicado na figura abaixo:
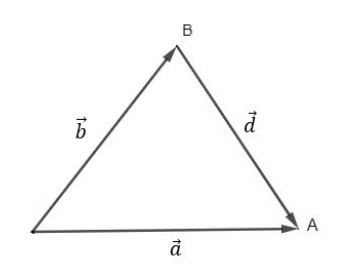
Algebricamente, podemos determinar que o módulo do vetor diferença será obtido determinado pela lei dos cossenos, desde que conhecido o ângulo entre os vetores:
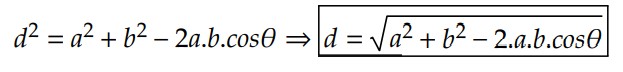
Note que existe uma pequena diferença no sinal da expressão do módulo do vetor diferença e a expressão do módulo do vetor soma.
Esse fato ocorre simplesmente por causa da geometria diferente dos dois problemas.
Quando o vetor é escrito em função das suas componentes, o vetor diferença é obtido de forma mais simples. Vamos mostrar para vetores no 𝑅3:
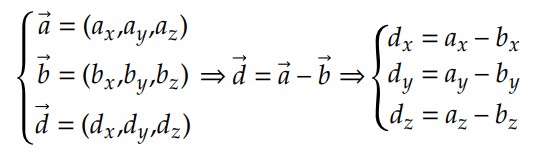
Essas são as operações mais comuns na matemática dos vetores.
Entretanto, existem duas operações, não tão trabalhadas comumente, mas que têm grande importância na Física. Vamos definir os dois tipos de produtos entre vetores. Diversas grandezas físicas são definidas utilizando essas operações.

Produto escalar
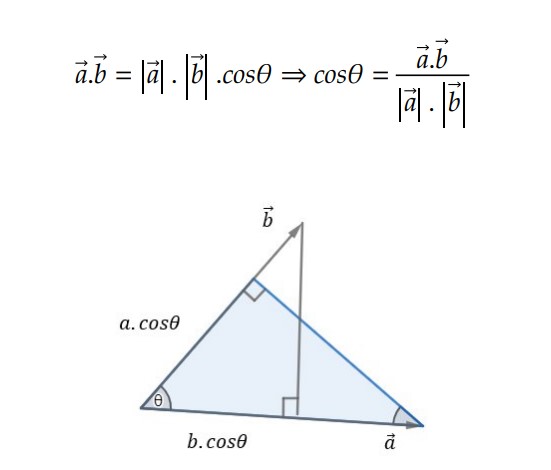
Define-se produto escalar entre 𝑎 e 𝑏 (escreve-se 𝑎.𝑏 e lê-se “a escalar b”) como a grandeza escalar cujo valor numérico é obtido multiplicando os módulos dos dois vetores operandos e também o cosseno do ângulo formado entre eles. Isto é:
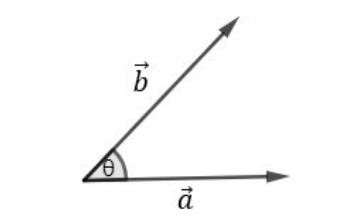
Primeiramente, é muito importante notar que essa operação resulta em um valor numérico. Fisicamente, esse produto entre duas grandezas vetoriais resulta em uma grandeza escalar. Alguns exemplos de grandezas escalares são: o trabalho de uma força, o potencial elétrico, o fluxo do campo elétrico, o fluxo do campo magnético etc.
Diante disso, precisamos saber trabalhar bem com produto escalar e, para isso, vamos ver algumas propriedades:

𝑎.𝑏 = 𝑏.𝑎
𝑎 (𝑏 + 𝑐) = 𝑎.𝑏 + 𝑎.𝑐
𝑎.𝑎 = |𝑎|2;
(𝑘𝑎).𝑏 = 𝑎.(𝑘𝑏) = 𝑘(𝑎.𝑏);
|𝑘𝑎| = |𝑘|. |𝑎|;
|𝑎.𝑏| ≤ |𝑎| |𝑏|, pois 𝑐𝑜𝑠𝜃 ≤ 1;
|𝑎 + 𝑏| ≤ |𝑎| + |𝑏|. Vamos fazer a demonstração dessa propriedade devido a sua utilidade.
Demonstração
Inicialmente, vamos fazer |𝑎 + 𝑏|2 = (𝑎 + 𝑏) . (𝑎 + 𝑏), usando a propriedade P3;
Em seguida, aplicando P4, temos que: |𝑎 + 𝑏|2 = (𝑎 + 𝑏) . (𝑎 + 𝑏) = 𝑎.𝑎 + 2.𝑎.𝑏 + 𝑏.𝑏;
Aplicando-se novamente a propriedade P3, temos que: |𝑎 + 𝑏|2 = 𝑎.𝑎 + 2.𝑎.𝑏 + 𝑏.𝑏 = |𝑎|2 + 2.𝑎.𝑏 + |𝑏|2;
Como 𝑎.𝑏 ≤ 𝑎.𝑏 – isto é, um número real é sempre menor ou igual ao seu módulo – e considerando a desigualdade de Cauchy-Schwarz, temos que:
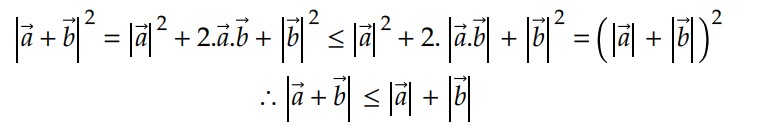
Verifica-se a igualdade nessa inequação quando 𝑐𝑜𝑠𝜃 = 1. Em outras palavras, quando os vetores são paralelos.
Pela definição, se o produto escalar de dois vetores – sendo 𝑎 ≠ 0 𝑒 𝑏 ≠ 0 com ângulo 𝜃 entre eles – é nulo, os vetores são perpendiculares:
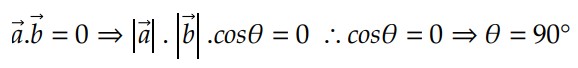
É imediato perceber que se um dos vetores é nulo, o produto vetorial dele com qualquer outro também será zero:
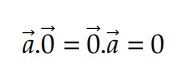
Pode-se mostrar que para dois vetores escritos em função de suas componentes – 𝑎 = (𝑎𝑥 ,𝑎𝑦 ,𝑎𝑧 ) e 𝑏 = (𝑏𝑥 ,𝑏𝑦 ,𝑏𝑧 ) -, seu produto escalar será dado por:
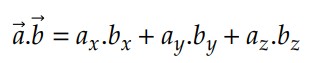
Isto é, o produto escalar será dado pelo produto das componentes do mesmo eixo. Dessa forma, pela definição, podemos calcular o ângulo entre dois vetores a partir do produto escalar:

Produto vetorial
Define-se o produto vetorial entre 𝑎 e 𝑏 como a grandeza vetorial cujo resultado também é um vetor perpendicular ao plano dos vetores operandos. Escreve-se 𝑎𝑥𝑏 (lê-se “a vetor b”).
Definição matemática: dados os vetores 𝑎 = (𝑎𝑥, 𝑎𝑦, 𝑎𝑧) e 𝑏 = (𝑏𝑥, 𝑏𝑦, 𝑏𝑧) de ℝ3, definimos o produto vetorial entre 𝑎 e 𝑏 como:
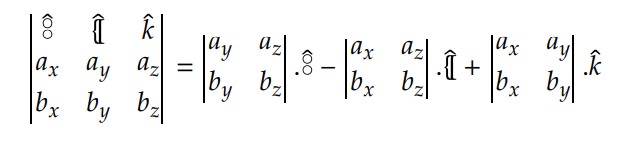
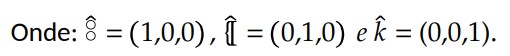
Para determinar o sentido do vetor resultante, utilizamos a regra da mão direita envolvente. Inicialmente, posiciona-se a mão direita na origem comum aos dois vetores e rotaciona-se no sentido do primeiro vetor (𝑎) para o segundo vetor (𝑏).
Então, o polegar da mão direita mostrará a direção do vetor resultante do produto vetorial 𝑎𝑥𝑏, como na figura abaixo:
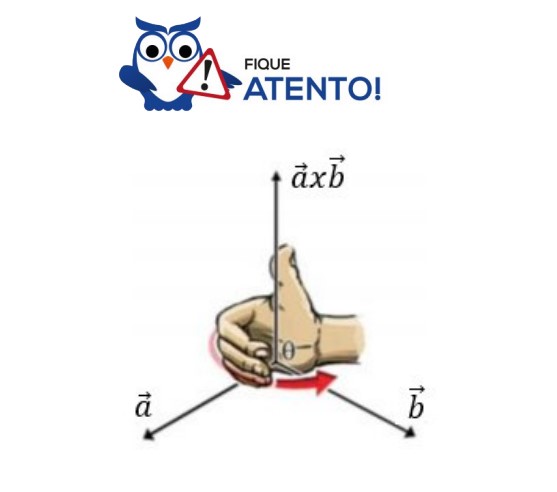
É fácil notar que para realizar a regra da mão direita é importante preocupar-se com a ordem dos vetores, pois isso altera a direção do vetor resultante.
Assim, podemos observar que: 𝑎𝑥𝑏 ≠ 𝑏𝑥𝑎. Ou seja, 𝑎𝑥𝑏 =− 𝑏𝑥𝑎. Sendo assim, não podemos aplicar a propriedade comutativa para produtos vetoriais.
Para determinar o módulo do produto vetorial entre 𝑎 𝑒 𝑏 usamos a expressão:
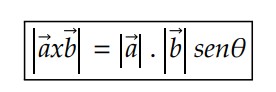
Algumas grandezas físicas importantes são definidas por um produto vetorial, tais como: velocidade angular, torque, força magnética que atua sobre uma carga puntiforme, entre outras.
Para melhorar nossos trabalhos com produto vetorial, vamos enumerar algumas propriedades:

Analisando geometricamente o módulo do produto vetorial entre 𝑎 e 𝑏, pode-se interpretar que ele é numericamente igual à área do paralelogramo formado pelos vetores 𝑎 e 𝑏, de acordo com a figura abaixo:
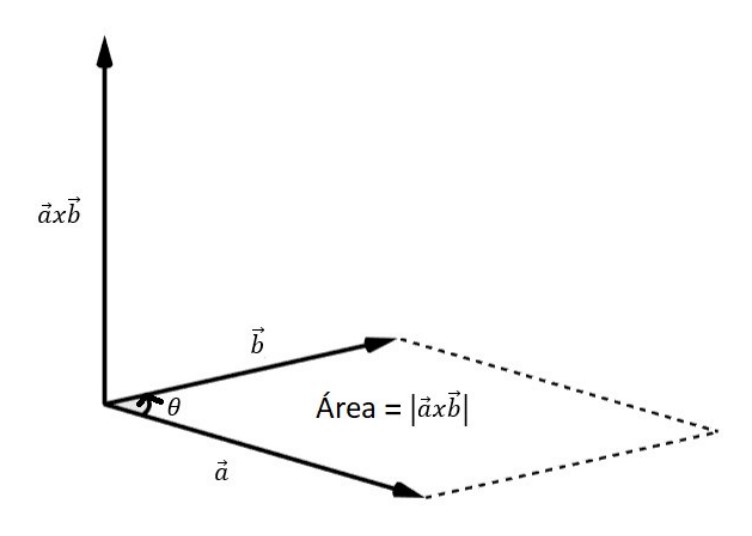
Dessa forma, sempre é possível associar uma área qualquer a um vetor.
Uma equação vetorial sempre nos mostra mais de uma informação, pois, a um vetor sempre está associado um módulo, uma direção e um sentido.
Gostou desta série sobre Vetores? Agora que chegamos ao seu fim, aproveite para estudar bastante e praticar o que aprendeu com exercícios e questões de provas de concursos anteriores. Conheça o Banco de Questões do Estratégia Militares e pratique ainda mais!
Veja também:
- Operações matemáticas com algarismos significativos
- Noções de Algarismos Significativos
- Cinemática Escalar: introdução
- Cinemática Escalar: velocidade escalar média, movimento progressivo e mais
- Física: introdução, grandeza, estudo e mais
- Movimento uniformemente variado: aceleração, cinemática com cálculo e mais!
- Movimento uniforme: o que é e para que serve?
Conteúdo didático elaborado pelo professor Toni Burgatto.



