Você que vai se candidatar a uma vaga em um Concurso Militar tem que ficar de olho nos conteúdos de Física! Eles costumam ser os mais difíceis dos certames. Por isso, o Estratégia Militares preparou um artigo sobre um tema importante: o Movimento Uniformemente Variado (MUV). Confira!
Já vimos, anteriormente, movimentos uniformes onde não existem aceleração tangencial. Isto quer dizer que o módulo da velocidade era constante, ou ainda, que a aceleração tangencial é constante e igual a zero.
Contudo, sabemos que, na realidade, a velocidade – ou módulo, ou direção, ou sentido – varia com o tempo. Diversos fenômenos ocorrem com aceleração ou desaceleração da velocidade.
Por exemplo, quando estamos viajando em uma rodovia, somos obrigados a acelerar e a desacelerar. Por isso, é fundamental estudarmos as causas e as consequências nessas variações de velocidade.
Navegue pelo conteúdo
Aceleração Escalar Média
Do mesmo modo que definimos a velocidade escalar média, podemos definir a aceleração escalar média:
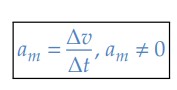
Ou ainda:
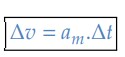
Como a variação de tempo é sempre positiva, o sinal da aceleração escalar média (𝑎𝑚) é o mesmo sinal da variação da velocidade (Δ𝑣).
Exemplo: Um carro parte do repouso e atinge a velocidade de 30 m/s em 10 segundos. Qual a sua aceleração escalar média nesse intervalo de tempo?
O móvel está inicialmente em repouso. Isto é, 𝑣0 = 0. Desta forma, a partir da definição, temos que:
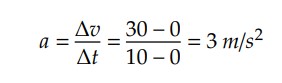
Aceleração Escalar Instantânea
De forma análoga ao pensamento da velocidade escalar instantânea, podemos definir a aceleração escalar instantânea como:

Da mesma forma, este limite mostra que a aceleração escalar instantânea é a derivada da velocidade escalar em relação ao tempo. Denota-se por:
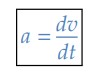
Diante disso, notamos que a derivada do espaço resulta na velocidade escalar instantânea e a derivada desta resulta na aceleração escalar instantânea:

Por exemplo: Dada a função horária da velocidade de um móvel definida por 𝑣 𝑡 = 10 + 4𝑡 − 5𝑡2, para determinarmos a aceleração, basta derivarmos:
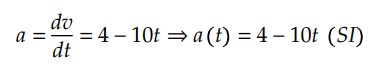
Notamos que, tanto na definição de aceleração escalar média quanto na definição de aceleração escalar instantânea, a aceleração escalar é definida como um quociente de velocidade pelo tempo. Então, a unidade de aceleração é dada por:
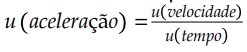
Logo, no SI, temos que a unidade de aceleração escalar é dada por:
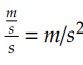
Movimentos acelerado e retardado
Veja as definições a seguir.
Movimento acelerado
Chamamos de movimento acelerado quando o módulo da velocidade escalar aumenta com o decorrer do tempo. Em outras palavras:
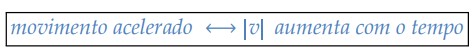
Como sabemos da teoria de módulo de um número real, 𝑣 pode ser maior ou menor que zero, mas sempre |𝑣| > 0.
Desta forma, existem dois tipos de movimentos acelerados:
1. Movimento acelerado é progressivo:
Nesse tipo de movimento 𝒗 > 𝟎 e se |𝑣| aumenta com o tempo, o mesmo acontece com 𝑣. Assim, Δ𝑣 é positivo, em qualquer intervalo de tempo, o que implica 𝒂 > 𝟎.
Exemplo: Um automóvel viajando na Dutra de São Paulo para Rio de Janeiro com velocidade escalar de 80 km/h passa para 100 km/h em alguns minutos.
A velocidade do móvel é positiva se adotarmos o eixo de São Paulo para o Rio de Janeiro. Portanto, sabemos que a velocidade é sempre positiva, o que nos mostra um movimento progressivo, pois o móvel está se deslocando na direção do aumento da posição 𝑠.
Ao calcularmos a variação da velocidade, encontramos que: Δ𝑣 = 𝑣2 − 𝑣1 = 100 − 80 = 20 𝑘𝑚/ℎ. Logo, Δ𝑣 > 0. Portanto, 𝑎𝑚 > 0. Dessa forma, temos o movimento acelerado progressivo: 𝑣 > 0 𝑒 𝑎 > 0.
2. Movimento acelerado é retrógrado:
Nesse tipo de movimento 𝒗 < 𝟎 e se |𝒗| aumenta com o tempo, então 𝑣 diminui. Assim, Δ𝑣 < 0 em qualquer intervalo de tempo, o que implica 𝒂 < 𝟎.
Exemplo: Agora vamos dizer que o carro está na Dutra indo do Rio de Janeiro para São Paulo, mas você não alterou o eixo da posição, de forma que o móvel tem uma velocidade – 80 km/h, que é negativa para indicar que está indo no sentido contrário ao adotado para o espaço 𝑠. Aplica-se uma aceleração no carro e chega a -100 km/h em alguns minutos.
Neste caso, trata-se de um movimento retrógrado, pois o móvel está na direção contrária ao eixo adotado pelo espaço, isto é, 𝑣 < 0. Além disso, podemos ver que Δ𝑣 =− 100 − (− 80) =− 20 𝑘𝑚/ℎ, ou seja, Δ𝑣 < 0, mas vimos que o módulo da velocidade aumentou (|− 100| > |− 80|). Assim, temos que no movimento acelerado retrógrado 𝒗 < 𝟎 e 𝒂 < 𝟎.
Podemos resumir da seguinte forma:
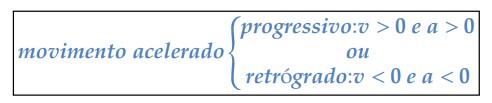
Assim, concluímos que no movimento acelerado 𝒗 e 𝒂 têm mesmo sinal. De outra forma, a expressão abaixo caracteriza o movimento acelerado:

Movimento retardado
Chamamos de movimento retardado quando o módulo da velocidade escalar diminui com o decorrer do tempo. Em outras palavras:
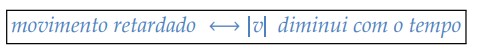
Como sabemos da teoria de módulo de um número real, 𝑣 pode ser maior ou menor que zero, mas sempre |𝑣| > 0. A partir disso, existem dois tipos de movimentos retardados:
1. Movimento retardado é progressivo:
Nesse caso 𝒗 > 𝟎 e se |𝒗| diminui com o tempo, então 𝑣 também o faz. Assim, Δ𝑣 é negativo, em qualquer intervalo de tempo, o que implica 𝒂 < 𝟎.
Exemplo: Um carro viajando na Dutra de São Paulo para Rio de Janeiro com velocidade escalar de 100 km/h passa para 80 km/h em alguns minutos.
A velocidade do móvel é positiva se adotarmos o eixo de São Paulo para o Rio de Janeiro. Portanto, sabemos que a velocidade é positiva, o que nos mostra um movimento progressivo, pois o móvel está se deslocando na direção do aumento da posição 𝑠.
Ao calcularmos a variação da velocidade, encontramos que: Δ𝑣 = 𝑣2 − 𝑣1 = 80 − 100 =− 20 𝑘𝑚/ℎ. Logo, Δ𝑣 < 0. Portanto, 𝑎𝑚 < 0. Dessa forma, temos o movimento retardado progressivo: 𝑣 > 0 𝑒 𝑎 < 0.
2. Movimento retardado é retrógrado:
Nesse caso 𝒗 < 𝟎 e se |𝒗| diminui com o tempo, então 𝑣 aumenta. Assim, Δ𝑣 > 0 em qualquer intervalo de tempo, o que implica 𝒂 > 𝟎.
Exemplo: Agora vamos dizer que o carro está na Dutra indo do Rio de Janeiro para São Paulo, mas você não alterou o eixo da posição, de forma que o móvel tem uma velocidade – 100 km/h, que é negativa para indicar que está indo no sentido contrário ao adotado para o espaço 𝑠. Aplica-se uma desaceleração no carro e chega-se a -80 km/h em alguns minutos.
Neste caso, trata-se de um movimento retrógrado, pois o móvel está na direção contrária ao adotado pelo espaço, isto é, 𝑣 < 0. Além disso, podemos ver que Δ𝑣 =− 80 – (− 100) =+ 20 𝑘𝑚/ℎ. Ou seja, Δ𝑣 > 0, mas podemos perceber que o módulo da velocidade diminuiu (|− 80| < |− 100|). Assim, temos que no movimento retardado retrógrado 𝒗 < 𝟎 e 𝒂 > 𝟎

Podemos resumir da seguinte forma:
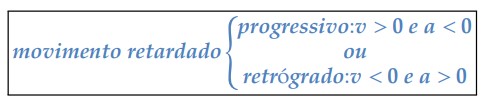
Assim, concluímos que no movimento retardado 𝒗 e 𝒂 têm sinais contrários. De outra forma, a expressão abaixo caracteriza o movimento retardado:
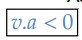
Agora, veremos movimentos onde existe mudança de velocidade causada por uma aceleração. No entanto, ainda nos restringiremos a mudanças uniformes nas velocidades, isto é, mudança de velocidade a uma taxa constante. Por isso, caracterizamos este movimento como uniformemente variado.
Assim, dizemos que o móvel sofre variações de velocidades iguais em intervalos de tempos iguais. Em outras palavras, dizemos que no MUV a aceleração escalar média também é a aceleração escalar instantânea, isto é:
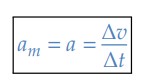
Assim, dizemos que o móvel sofre variações de velocidades iguais em intervalos de tempos iguais.

Quando a trajetória do MUV for uma reta chamamos de MRUV – Movimento Retilíneo Uniformemente Variado. Quando a trajetória do MUV for uma circunferência, chamamos de MCUV – Movimento Curvilíneo Uniformemente Variado.
Função horária da Velocidade no MUV
Neste movimento, temos como principal característica:
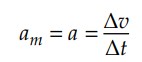
Se um móvel com velocidade 𝑣0 no instante 𝑡0 passa a ter uma velocidade 𝑣 em um instante 𝑡, podemos escrever que:
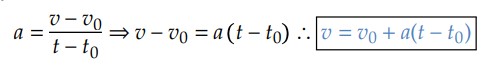
Para simplificar nossa vida, vamos contar o início do movimento na origem dos tempos, isto é, 𝑡0 = 0. Então:
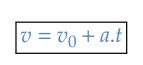
A partir desse resultado, podemos concluir que:
- a função horária da velocidade no MUV é uma função do primeiro grau em 𝑡;
- 𝑣0 é a velocidade para o instante 𝑡 = 0, sendo o coeficiente linear da nossa função do primeiro grau em 𝑡;
- 𝑎 é a aceleração escalar instantânea diferente de zero, sendo o coeficiente angular da nossa função do primeiro grau em 𝑡. O valor de |𝑎| é quem determina a taxa de crescimento ou a diminuição da nossa velocidade; e
- 𝑣 é a velocidade em um dado instante 𝑡.
Função horária do espaço no MUV
Para chegarmos à função horária do espaço no MUV, vamos utilizar o caso de um móvel com velocidades positivas e aceleração positiva, isto é, descrevendo um movimento acelerado progressivo.
Sem perdas de generalidade, podemos desenhar o gráfico da função horária de sua velocidade da seguinte forma:
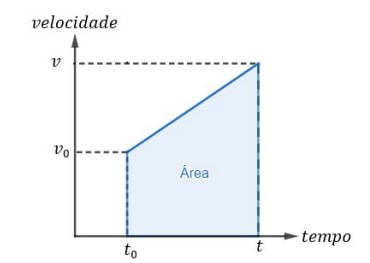
Para a dedução da função horária do espaço no MUV vamos utilizar o conceito de áreas de gráficos na cinemática. A área azul do gráfico de 𝑣 × 𝑡 é numericamente igual à variação do espaço para o tempo correspondente, isto é:

Nossa área em questão é um trapézio retângulo com base menor igual a 𝑣0, base maior igual a 𝑣 e altura igual a Δ𝑡 = 𝑡 − 𝑡0. Assim:
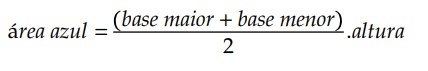

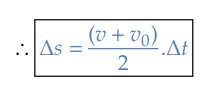
Essa relação é extremamente importante para a dedução de algumas equações. Vamos chamá-la de equação coringa.
No MUV, sabemos que a velocidade obedece à seguinte equação: 𝑣 = 𝑣0 + 𝑎(𝑡 − 𝑡0). Logo:
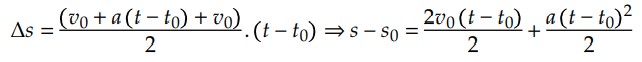
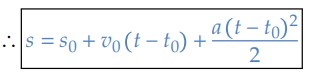
Ou ainda, quando tomamos a contagem do tempo na origem dos tempos – ou seja, 𝑡0 = 0 – temos finalmente que:
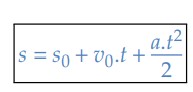
Dessa forma, a função horária do espaço no MUV é uma função do segundo grau em 𝑡 (𝑎 ≠ 0), onde:
- 𝑠0 é o espaço inicial quando 𝑡 = 0;
- 𝑣0 é a velocidade inicial, isto é, velocidade para 𝑡 = 0;
- 𝑎 é a aceleração escalar instantânea; e
- 𝑠 é o espaço para um dado instante 𝑡.
Notamos que 𝑠0, 𝑣0 𝑒 𝑎 são constantes no MUV.
Neste momento observamos que, conhecendo a função horária do espaço, podemos determinar a função horária da velocidade, além de podermos determinar a aceleração do movimento.
Teoria de Cinemática com cálculo
Para começar esta segunda parte do estudo, vamos dar uma pausa na teoria de Movimento Uniformemente Variado (MUV) e ver um pouco mais da teoria de Cinemática com cálculo.
Ela nos diz que a velocidade escalar instantânea é a derivada do espaço em relação ao tempo. Se aplicarmos esse conceito, podemos dizer que:
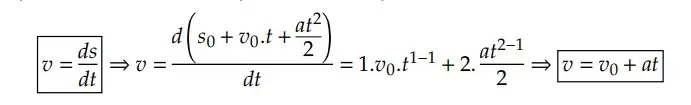
Vale lembrar que a derivada de uma constante é zero e 𝑠0 é constante.
Da mesma forma, sabemos que a aceleração escalar instantânea é a derivada da velocidade em relação ao tempo. Ou seja:
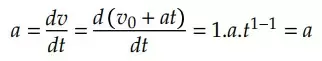
Tudo conforme o seguinte critério:
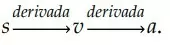
Por outro lado, dada a função horária da velocidade, para determinar a função horária do espaço, é necessário fazer o processo inverso da derivação – isto é, fazer uma integração.
Para o caso de funções polinomiais, basta pensarmos no processo inverso para cada termo. Para o MUV, dado 𝑣 = 𝑣0 + 𝑎𝑡, podemos extrair quem são 𝑣0 e 𝑎.
Depois, para escrever a função de 𝑠, você precisa saber alguma informação sobre a posição inicial (𝑠0) e, assim, determinar completamente a função horária do espaço.
Para o caso da função horária da velocidade não ser de um MUV – por exemplo, 𝑣 = 2𝑡 + 3𝑡2 – vamos resolver o problema de maneira informal.
Não vamos ser rigorosos na matemática, mas apenas no operacional para encontrar a nossa resposta.

Dizemos que:
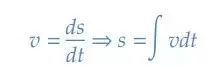
Não se assuste com este símbolo, é apenas mais um sinal matemático. Aqui, só precisamos nos atentar para o caso dele integrar uma função polinomial, do tipo 𝑓 (𝑥) = 𝑎0 + 𝑎1𝑥 + 𝑎2𝑥2 + … + 𝑎𝑛𝑥𝑛.
Assim, escrevemos que 𝑠 =∫ (2𝑡 + 3𝑡2) 𝑑𝑡 e pensamos no processo inverso. Quando existia a função 𝑠 e derivamos para saber 𝑣, usamos a regra do tombo e eliminamos a constante.
Agora vamos elevar o grau do expoente e dividir o número pelo grau do expoente para o qual o termo foi.
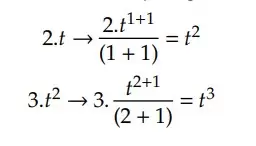
Além disso, devemos adicionar uma constante de integração – pois ao derivar, eliminamos a constante – o espaço inicial. Desta forma, temos que a função horária do espaço é dada por:
𝑠 = 𝑠0 + 𝑡2 + 𝑡3
Note que, ao derivarmos a expressão de 𝑠, chegaremos em 𝑣 conforme o enunciado do exemplo.
Se quisermos a aceleração, basta derivarmos a velocidade:
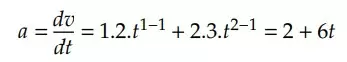
Cálculo da Velocidade Média no MUV
Apenas no Movimento Uniforme (UM) a velocidade escalar média (𝑣𝑚) é igual à velocidade escalar instantânea (𝑣). Entretanto, o conceito de velocidade não muda no MUV:
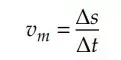
Desta forma, podnnotation”>emos usar nossa equação coringa para calcular de forma simples a velocidade média no MUV:
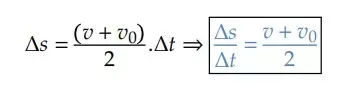
Ao analisarmos essa última relação, apenas manipulando algebricamente a equação coringa, podemos observar que para dois instantes genéricos (𝑡 = 0 e 𝑡), a velocidade escalar média é a média aritmética das velocidades escalares instantâneas nos correspondentes instantes, então:


Neste momento não podemos confundir as condições do MU e do MUV. No MU não podemos simplesmente calcular a velocidade média entre dois instantes como a média aritmética das velocidades. Apenas para trechos iguais calculamos a velocidade escalar média como a média harmônica das velocidades de cada trecho.
No MUV, a velocidade escalar média em dois instantes é, sim, a média das velocidades para esses dois instantes. Para o caso da velocidade instantânea variar de forma não linear com o tempo, a velocidade média deverá ser unicamente calculada pela forma tradicional:
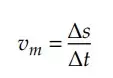
Graficamente, temos que:
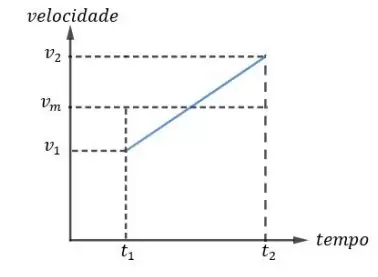
Vamos calcular a área do trapézio (𝐴𝑡𝑟𝑎pézio) retângulo definido por 𝑣1, 𝑣2, 𝑡1 𝑒 𝑡2, e a área do retângulo (𝐴𝑟𝑒tângulo) delimitado por 𝑣𝑚, 𝑡1 𝑒 𝑡2. Logo:
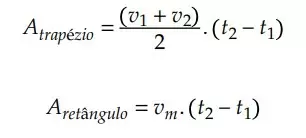
Como:

temos que:
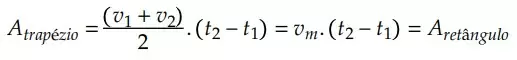
Isto é, calcular a velocidade escalar média é obter uma velocidade que satisfaça a condição do móvel percorrer a mesma variação de espaço no intervalo de tempo correspondente.
A equação de Torricelli
Novamente, vamos utilizar a função horária da velocidade e isolar o Δ𝑡, com o objetivo de encontrar uma equação que relaciona velocidade, aceleração e deslocamento, sem ter o tempo como termo da equação:
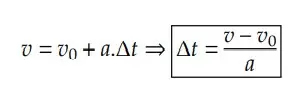
Observação: como estamos no MUV, a aceleração escalar instantânea é diferente de zero. Logo, não há problemas em fazer essa manipulação matemática. A partir do resultado, vamos utilizar novamente nossa equação coringa e substituir o Δ𝑡 que acabamos de encontrar:
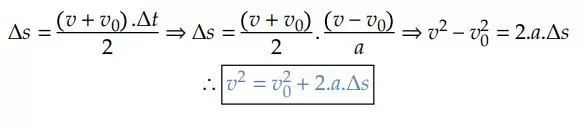

Discussão dos sinais da velocidade escalar v quando usamos Torricelli
Quando utilizamos a equação de Torricelli, a primeira dúvida que surge é com relação ao sinal da velocidade, pois:
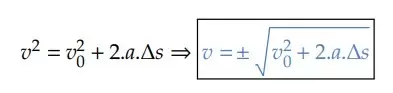
Assim, obtivemos duas possíveis velocidades escalares: uma positiva e outra negativa. No entanto, escolher, dentre as duas, qual será a velocidade do móvel dependerá da orientação da trajetória e do tipo de movimento: acelerado ou retardado.
Movimento acelerado
- Movimento progressivo: Para o movimento acelerado, o móvel passará por B uma única vez e terá velocidade positiva se estiver se movimentando no sentido da trajetória. Portanto:
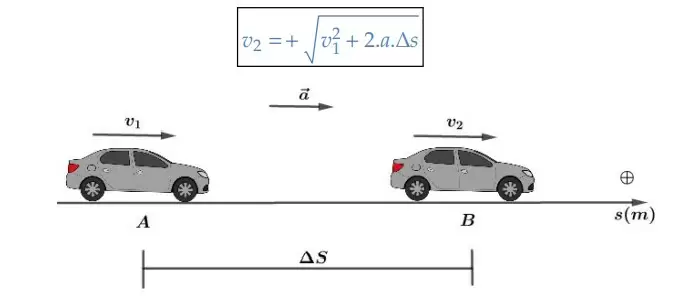
- Movimento retrógrado: Se o móvel estiver se deslocando no sentido contrário da trajetória (movimento retrógrado) e for acelerado, então passará por B ou por A uma única vez e sua velocidade será negativa:
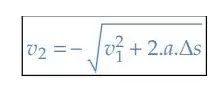
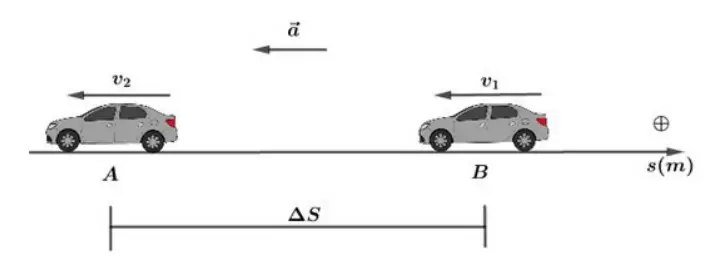
Note que a aceleração é negativa, mas a variação do espaço também, de forma que o produto 𝑎.Δ𝑠 será positivo. Portanto, 𝑣 aumentará. Uma característica do movimento acelerado.
Movimento retardado
- Inicialmente progressivo: Analisando o movimento retardado, se inicialmente o móvel vai de A para B (sentido da trajetória) sabemos que sua velocidade é positiva, mas sua aceleração será negativa, então nesse intervalo, o móvel possui velocidade positiva. Logo, utilizamos:

Entretanto, sabemos que a velocidade está diminuindo devido ao fato da aceleração estar em sentido contrário ao da velocidade – até chegar o momento em que ela se anula e o móvel muda de sentido. A característica da mudança de sentido é o fato da velocidade ser nula nesse instante.
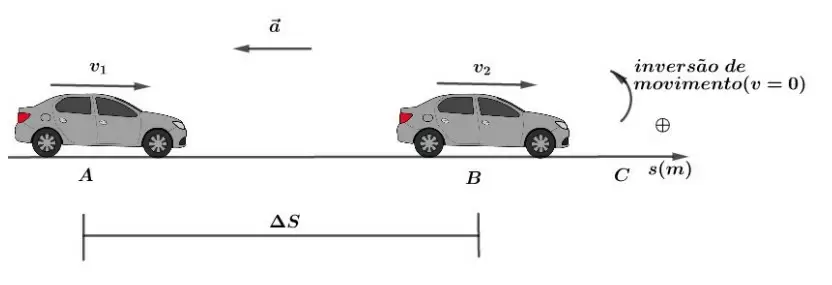
Note que o produto 𝑎∙Δ𝑆 < 0, logo |𝑣2| < |𝑣1|. Após esse momento, o movimento passa a ser retrógrado acelerado, isto é, ele vai para a esquerda acelerado, portanto, sua velocidade será negativa:
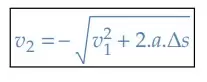
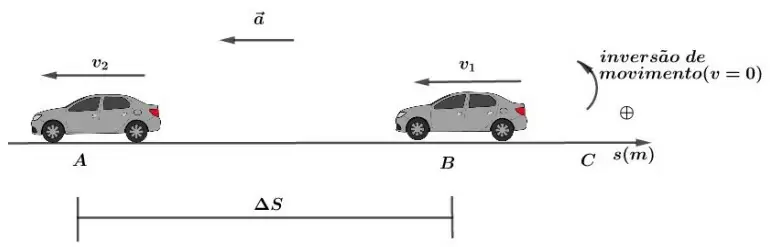
Nesse caso, temos que o movimento é retrógrado acelerado e o produto 𝑎.Δ𝑠 será positivo. Isto é, 𝑣 aumenta nessa fase do movimento.
- Inicialmente retrógrado: Agora, se o móvel se desloca no sentido de B para A (contrário a trajetória, movimento retrógrado) mas retardado – ou seja, sua velocidade vai diminuindo de B para A, pois a aceleração é contrária à velocidade – o móvel chegará novamente ao momento em que inverte seu sentido. Até esse momento, sua velocidade será negativa (contrária ao movimento), dado por:
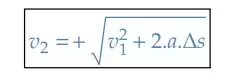
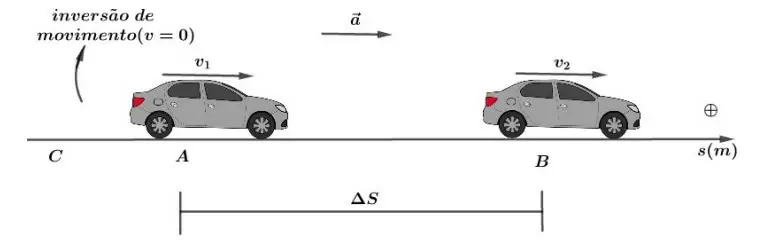
Notamos que a aceleração é positiva e a variação do espaço é positiva, logo, o produto 𝑎.Δ𝑠 será positivo. Portanto, |𝑣| aumenta nessa fase do movimento, conforme visto na teoria anteriormente.
Movimento Vertical no vácuo
Segundo a história, por volta de 1590, Galileu Galilei realizou um experimento na torre de Pisa que o tornou famoso. Ele subiu no alto da torre e abandonou simultaneamente duas pequenas esferas de pesos diferentes – e elas chegaram juntas ao solo.
Galileu ainda observou que, para variações de tempos iguais, as variações de espaços das esferas não eram linearmente proporcionais às de tempo. Isto é, o movimento era acelerado e, ainda, elas estavam sempre lado a lado, chegando ao solo juntas, conforme a figura abaixo:
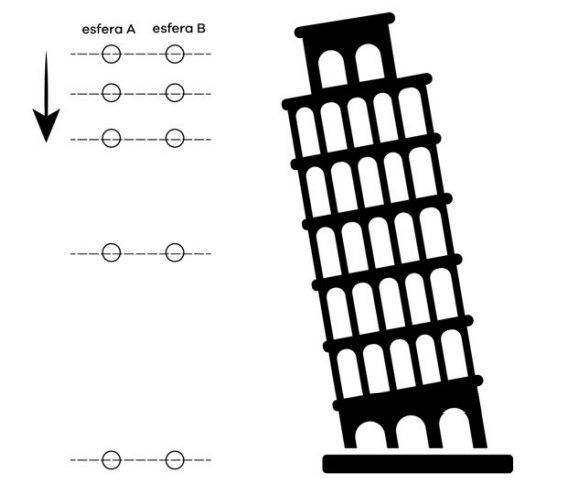
Hoje sabemos que o resultado obtido por Galileu é verdadeiro somente se abandonarmos os corpos em queda livre, ou seja, no vácuo ou num local desprovido de qualquer resistência.
Dessa forma, concluímos que, próximo à superfície da Terra, todo corpo em queda livre tem aceleração constante. Ela é chamada de aceleração da gravidade ou aceleração gravitacional, onde o módulo é representado pela letra 𝑔.
A aceleração da gravidade varia com o raio da Terra, com a latitude e com a altitude. Para o estudo de queda livre os problemas geralmente estão delimitados em regiões pequenas, onde os fatores que alteram a gravidade pouco influenciam na mudança. Por isso, consideramos a aceleração da gravidade constante.
Muitas vezes os exercícios fornecem o módulo da aceleração da gravidade, outras vezes você deve apenas considerar que o módulo é 𝑔 e, em alguns casos, é aconselhado usar |𝑔| = 10𝑚/𝑠2 para facilitar as contas na questão.
Neste momento, vamos dizer que a aceleração da gravidade está orientada para o centro da Terra. Logo, para os corpos se movimentando na vertical próximo da Terra, adotamos que a aceleração gravitacional está sempre apontando para baixo, na direção do centro da Terra.
Dessa forma, se lançamos um objeto para cima, ele terá velocidade para cima e aceleração da gravidade para baixo durante a subida, ou seja, o objeto está em um movimento retardado, até chegar no ponto onde a velocidade vertical dele se anula.
Após esse instante, o objeto inverte sua trajetória e passa a ser acelerado para baixo, aumentando novamente o módulo da velocidade, como visto na figura abaixo:
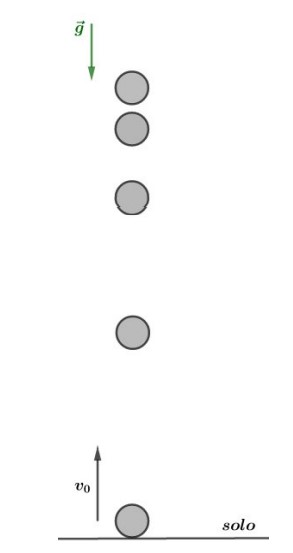
Consideração: No nosso estudo de lançamento vertical, não levamos em consideração outros movimentos que existem, como a rotação da Terra, ventos e resistência do ar. Por isso, podemos afirmar nossa trajetória apenas na vertical.
Como dito anteriormente, para resolvermos os problemas de cinemática, sempre adotamos uma orientação para a trajetória e verificamos os sinais das nossas grandezas físicas de acordo com essa orientação.
Neste movimento, sempre vamos adotar uma orientação a nosso critério e, a partir disso, escrever nossas equações matemáticas que representam o fenômeno físico da questão.
Existem duas orientações possíveis, entretanto, falaremos apenas da orientação positiva para cima para você não se confundir nos estudos.
Orientação positiva para cima
Quando o móvel está subindo, sua velocidade é positiva (𝑣 > 0, sentido da trajetória) mas a aceleração da gravidade é para baixo. Logo, teremos um movimento retardado progressivo (𝑣.𝑎 < 0).
Fisicamente, isso mostra que o módulo da velocidade (|𝑣|) da bolinha está diminuindo – ou seja, ela está sendo freada até que chegue em um ponto onde sua velocidade é zero.
Nesse ponto, dizemos que a bolinha atingiu a altura máxima, pois, a partir desse instante, ela terá velocidade negativa (𝑣 < 0), indicando que ela inverteu o sentido do movimento (orientação da trajetória para cima).
Em seguida, a bolinha começa a descer, isto é, ela está sendo acelerada para baixo. Assim, o módulo da velocidade (|𝑣|) começa a aumentar à medida que ela está descendo, iniciando-se assim o movimento acelerado retrógrado (𝑣.𝑎 > 0).
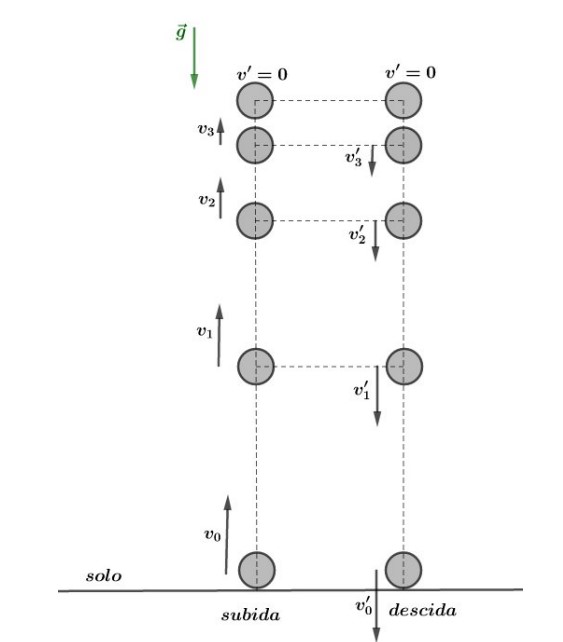
Assim, para o movimento vertical no vácuo, vamos utilizar nossas equações do MUV, com as devidas alterações para se encaixar no movimento do problema.
Altura Máxima
Vamos estudar o lançamento vertical de um corpo a partir do solo, com velocidade inicial 𝑣0 e sujeito exclusivamente à ação da gravidade durante o movimento. Isto é, vamos desprezar quaisquer resistências.
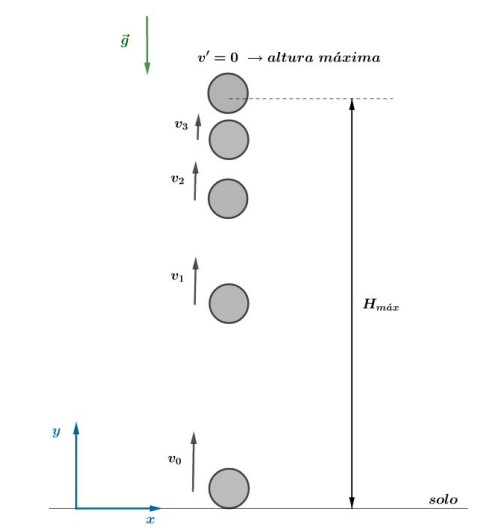
A altura máxima que o corpo pode atingir, quando lançado com uma velocidade 𝑣0, pode ser determinada diretamente pela equação de Torricelli, da seguinte maneira:
𝑣2 = 𝑣2 + 2.𝑎.Δ𝑠
Onde:
1) 𝑎 = − 𝑔, pois a aceleração da gravidade é contrária ao sentido adotado;
2) 𝑣0 > 0, pois quando lançamos a velocidade está na direção da orientação;
3) Δ𝑠 > 0, dado que a orientação é para cima, o deslocamento vertical pode ser escrito como Δ𝑠 = ℎ𝑚á𝑥 − ℎ0, em que ℎ0 está situado na origem do eixo adotado, portanto, ℎ0 = 0;
4) 𝑣 = 0, pois quando a bolinha atinge a altura máxima, sua velocidade é nula (característica de inversão de trajetória).
Dessa forma, temos que:
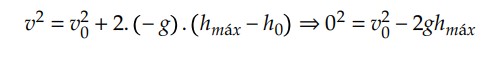
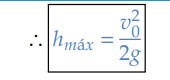
Tempo de subida até a altura máxima
Para determinar o tempo de subida, precisamos de uma equação que relaciona tempo e alguma informação que já temos. Dessa forma, a função horária da velocidade é perfeita para determinar o tempo de subida, pois sabemos que a velocidade escalar quando atinge a altura máxima é nula. Logo:
𝑣 = 𝑣0 + 𝑎.𝑡
A aceleração da gravidade aponta para baixo, logo, 𝑎 = − 𝑔. Então
𝑣 = 𝑣0 − 𝑔.𝑡 ⇒ 0 = 𝑣0 − 𝑔.𝑡𝑠𝑢𝑏𝑖𝑑a
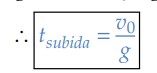
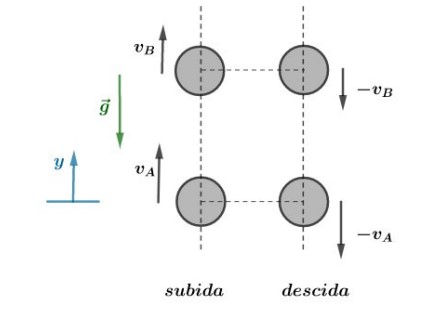
Tempo de subida e de descida entre os pontos A e B
Vamos tomar dois pontos da vertical A e B, como visto abaixo:
Pela função horária da velocidade, podemos escrever a equação da velocidade em B a partir do ponto A no momento de subida, isto é:
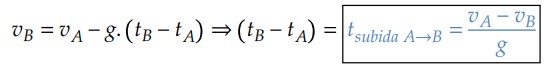
No momento da descida, o corpo vai de B para A, sentido contrário à orientação adotada, logo:
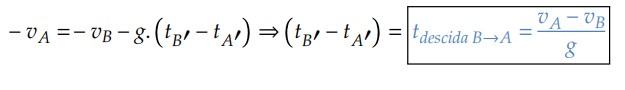
Dessa forma, vemos que entre dois pontos da trajetória, o tempo de subida é igual ao tempo de descida, isto é, o movimento é simétrico.
Então, o tempo de subida até a altura máxima é igual ao tempo de descida da altura máxima até o solo, ou seja:
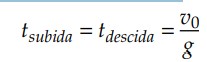
Logo, o tempo total de voo do corpo lançado do solo para cima com velocidade escalar 𝑣0 no vácuo é dado por:

Velocidade V para uma altura H qualquer
Para um corpo lançado verticalmente para cima, com velocidade inicial 𝑣0, podemos determinar a velocidade a uma altura h pela equação de Torricelli.
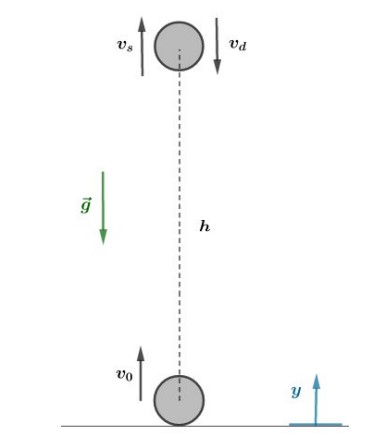
Se orientarmos a trajetória para cima, podemos aplicar Torricelli:
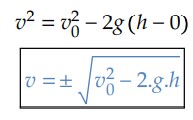
Quando esquematizamos dessa forma, existem dois valores possíveis para velocidade, pois existem dois momentos possíveis onde o corpo pode estar a uma altura h. O primeiro é quando o corpo está subindo e passa por h e o segundo quando o corpo está descendo.
Entretanto, podemos afirmar que o módulo da velocidade é o mesmo na subida e na descida quando passa por h. Assim, determinar o sinal dependerá da condição do problema, mas dada nossa orientação, já sabemos que:
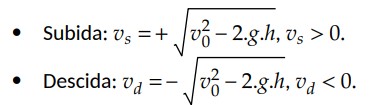
Gostou desse conteúdo sobre o MUV? Ele pode ajudar você a conquistar a sua vaga nas Forças Armadas! E os cursos do Estratégia Militares também. Se você quer se tornar um militar de carreira não perca mais tempo! Clique no banner e conheça nossos cursos!
Se você deseja se tornar um militar de carreira, não deixe de conhecer os cursos do Estratégia Militares. Nós somos líderes no que vale: classificação. Clique no banner e saiba mais!
Veja também:
- Operações matemáticas com algarismos significativos
- Noções de Algarismos Significativos
- Cinemática Escalar: introdução
- Cinemática Escalar: velocidade escalar média, movimento progressivo e mais
- Física: introdução, grandeza, estudo e mais
Conteúdo didático elaborado pelo professor Toni Burgatto.



