Estudando para entrar nas escolas militares? Confira os resumos que o Estratégia Militares preparou sobre os assuntos mais cobrados nos seletivos! Contamos a você o que é uma Progressão Geométrica (PG), suas propriedades e muito mais.
Antes de começarmos, que tal assinar nossa Newsletter? Trazemos semanalmente as principais notícias do mundo dos concursos militares, dicas de carreira e curiosidades!
Navegue pelo conteúdo
O que são Sequências?
Antes de definir a Progressão Geométrica, tenha em mente que ela é um tipo de sequência – uma série de números naturais que correspondem a um número real ou complexo. Existem alguns tipos delas, sendo que os mais conhecidos são a própria PG e a Progressão Aritmética (PA).
Em uma sequência, o termo é dado como ?n, sendo que n equivale à posição do termo e é sempre um número natural. De forma que a notação da sequência se apresenta da seguinte forma:
(?1,?2,?3,…,?n)
As sequências seguem uma lógica, chamada de Lei de Formação. Ela permite calcular qualquer termo de uma sequência levando em conta a posição dele, ou seja, o n.
Para entender mais sobre o que são Sequências e a PA, visite “Progressão Aritmética: o que é, tipos e propriedades”.
O que é uma Progressão Geométrica?
Uma Progressão Geométrica é uma sequência com a seguinte Lei de Formação:
?? = ?
?? = ??−?.?
Em outras palavras, você sempre multiplica o termo anterior por um mesmo valor para obter o número seguinte da sequência. Esse valor recebe o nome de razão e é representado por q.
Confuso? Confira alguns exemplos:
- (1, 3, 9, 27, …). PG cujo primeiro termo é ?1 = 1 e sua razão é:
. PG com ?1 = 1 e razão:
3) (3, − 9, 27, − 81,…). PG com ?1 = 3 e razão:
Como encontrar o Termo Geral da PG?
Se você quiser encontrar um termo da PG pela posição que ele ocupa, você pode calcular o termo geral da PG por meio da fórmula de recorrência. Para entender o raciocínio, escreva os termos da seguinte forma:
?2 = ?1.?
?3 = ?2.?
?4 = ?3.?
?5 = ?4.?
⋮
?? = ??−1.?
Perceba que temos ? − 1 termos. Vamos multiplicá-los:
Os termos em vermelho se cancelam e assim obtemos o termo geral da PG:
?? = ?1.??−1
Também podemos escrever o termo geral em função de um termo qualquer da PG. Usando o termo geral, podemos escrever:
?? = ?1.??−1
?? = ?1.??−1
Dividindo as duas equações:
?? = ??.? (?−1) −(?−1)
?? = ??. ? (?−?)
Quais as propriedades de uma PG?
Assim como a PA, a PG também conta com algumas propriedades que facilitam na hora de calcular os resultados procurados.
Termos Equidistantes
A primeira propriedade aponta que o produto dos termos equidistantes é um valor constante e a soma dos índices é igual à ? + 1. Para prová-la, vamos escrever os termos equidistantes generalizados ??+1 e ??−?, ?∈ℕ, usando o termo geral da PG.
??+1 = ?1. ? (?+1) −1 = ?1. ??
??−? = ?1. ? (?−?) −1
Multiplicando os dois termos, temos:
??+1.??−? = (?1.??) (?1 ? (?−?) −1)
??+1 .??−? = ?1 .?1 .?? .? [(?−?) −1]
??+1 .??−? = ?1 .?1 .??−1
Sabemos que ?? = ?1. ??−1, substituindo na equação acima:
??+1 .??−? = ?1 .??
Logo, o produto dos termos equidistantes é igual ao valor do produto dos extremos.
Soma dos termos de PG finita
Se uma PG for finita, é possível calcular a soma de todos os seus termos por meio da seguinte fórmula:
Para chegar nela é preciso seguir o raciocínio a seguir. Primeiro, escreva a soma da PG finita:
?? = ?1 + ?2 + ?3 + … + ??−1 + ??
Se usar o termo geral para escrever os termos:
?2 = ?1.?
?3 = ?1 .?2
?4 = ?1. ?3
⋮
?? = ?1 .??−1
Agora, substituímos os termos em Sn:
?? = ?1 + ?1? + ?1 .?2 + ?1 .?3 + … + ?1 .??−1
Multiplicando ?? por ?, obtemos:
?.?? = ?1.? + ?1 ?2 + ?1 ?3 + ?1. ?4 + … + ?1 ??
Subtraindo as duas equações:
?? − ?.?? = ?1 + ?1? + ?1 ?2 + ?1 ?3 + … + ?1 ??−1 − (?1? + ?1 ?2 + ?1 ?3 + ?1 ?4 + … + ?1 .??)
Repare que os termos em negrito se cancelam. Dessa forma:
?? − ?.?? = ?1 − ?1 .??
?? (1 − ?) = ?1 (1 − ??)
Também podemos escrever:
Soma dos termos de PG infinita
Se a PG for infinita, no entanto, e a razão absoluta for menor que 1, a soma dos seus termos converge para a1/(1-q), como demonstrado na fórmula a seguir, com 0<|q|<1:
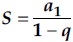
Observe a demonstração:
(?1,?2,?3,…) ?? ????????
Vamos escrever a fórmula da soma da PG finita:
Se − 1 < ? < 1 e a PG é infinita podemos escrever:
Ainda está confuso? Observe a sequência a seguir:
Perceba que os valores vão diminuindo à medida que o índice aumenta. Vamos calcular ?10:
Se tentarmos calcular ?? tal que ? seja tão grande, vamos obter um valor muito próximo de zero. Assim, quando ? tende ao infinito, podemos escrever:
Essa propriedade é válida para números pertencentes ao intervalo ] − 1, 1[.
Produto dos termos da PG
Outra propriedade é a multiplicação dos termos da PG. A fórmula é:
Entenda como ela é obtida! Primeiro, escreva os termos da PG usando o termo geral:
?1 = ?1
?2 = ?1.?
?3 = ?1. ?2
?4 = ?1 ?3
⋮
?? = ?1 .??−1
Multiplicando os termos da PG, obtemos:
?? = ?1? ?1+2+3+..+ (?−1)
1 + 2 + 3 + … + (? − 1) é uma soma de PA de razão 1. Aplicando a fórmula da soma da PA:
Substituindo em ??:
No caso de n ser ímpar, podemos escrever também:
Note que é o termo médio da PG. Para provar essa afirmação, fazemos da seguinte forma:
Pela fórmula dos produtos dos termos da PG, temos:
Tome nota!
O produto dos termos de uma sequência também pode ser representado dessa forma:
Π é o símbolo usado para representar o produtório de uma sequência. Ela parte do termo de índice ? = 1 e vai até o termo de índice ?.
Média Geométrica
Por meio da Média Geométrica conseguimos expressar os termos sem usar a razão. Como assim? Representando ??−1 e ??+1 usando o termo geral da PG:
??−1 = ?1 .? (?−1) −1 = ?1 .??−2
??+1 = ?1 .? (?+1) −1 = ?1 .??
Multiplicando os termos, obtemos:
??−1 .??+1 = ?1 .??−2 .?1 .?? = ?12 .?2?−2 = ?12 ?2(?−1) = [?1 .??−1] 2 = ??2
⇒ ??−1 .??+1 = ??2
Assim, para uma PG (?1,?2,?3), podemos escrever ?2 como a média geométrica de ?1 e ?3:
??? = ?? .??
Notação Especial
Outra forma de escrever uma PG é da seguinte forma:
PG com 3 termos:
PG com 4 termos:
PG com 5 termos:
Note que a razão da PG com 4 termos é ? = ?2.
Progressão Aritmética Geométrica (PAG)
Entre as sequências, também podemos ter uma que é a união de uma PA com uma PG. Essa sequência chama-se progressão aritmética geométrica (PAG). A definição de seu termo geral é dada por:
?? = [?? + (? − ?) ?] ??−?
Veja os exemplos:
Perceba que o numerador é uma PA de razão 1 (1, 2, 3, 4, 5,…) e o denominador é uma PG de razão 2 (1, 2, 4, 8, 16,…) . Essa sequência é uma PAG.
Para a PAG, a razão ? é igual a 1 e a razão ? é igual a 1/2. O termo geral é:
?? = [?1 + (? − 1) ?] ??−1
As questões que podem cair na prova sobre PAG normalmente cobrarão a soma dos termos da PAG. Vamos aprender a resolver esse tipo de questão.
Considere o termo inicial da PAG ?1 = ? e razões ? e ?. Vamos calcular:
? = ? + [(? + ?) ?] + [(? + 2?) ?2] + [(? + 3?) ?3] + …
O bizu dessa questão é multiplicar ? por ? e fazer ? − ??. Veja:
?? = ?? + [(? + ?) ?2] + [(? + 2?) ?3] + [(? + 3?) ?4] + …
Fazendo ? − ??:
? − ?? = ? + [(? + ?) ?] + [(? + 2?) ?2] + [(? + 3?) ?3] + …
− {?? + [(? + ?) ?2] + [(? + 2?) ?3] + [(? + 3?) ?4 + …}
Repare que os termos em negrito, itálico e sublinhados de forma semelhante podem ser subtraídos. Dessa forma, obtemos:
? (1 − ?) = ? + ?? + ??2 + ??3 + ??4 + …
Encontramos uma fórmula para a soma de uma PAG de razão − 1 < ? < 1.
Hora de praticar!
Com o conhecimento básico de PG em mente, que tal testar o que aprendeu? Resolva o exercício abaixo:
Dado a PG (?, − ?, ?, − ??, ??,…), calcule:
a) ???
b) ???
Resolução:
a) Para calcular os termos da PG, precisamos encontrar sua razão. Podemos aplicar a fórmula de recorrência:
Observando a sequência, ?2 = − 4 e ?1 = 2. Substituindo na fórmula acima:
Usando o termo geral para calcular ?20:
?20 = ?1 .?20−1 = ?1 .?19
?20 = 2 (− 2) 19 = − 220
b) Conhecemos a razão e o termo inicial, vamos aplicar o termo geral:
?30 = ?1 .?30−1 = ?1 .?29
?30 = 2 (− 2) 29 = − 230
Gostou do conteúdo? Acompanhe o Portal do Estratégia Militares e tenha acesso a mais resumos dos nossos professores! Além disso, se quiser treinar ainda mais seus conhecimentos, assine o Banco de Questões do Estratégia Militares!
São milhares de questões dos mais variados níveis, tanto inéditas quanto de concursos anteriores, para você aproveitar! Clique no banner e saiba mais!




