Se você está estudando para os concursos militares, fique ligado nos resumos que o Estratégia Militares preparou sobre os assuntos mais cobrados nos seletivos! Neste artigo de matemática, conheça o tipo de sequência conhecido como Progressão Aritmética (PA) e suas propriedades.
Navegue pelo conteúdo
O que são Sequências?
Antes de explicar o que é a própria PA, é preciso ter em mente que ela é um tipo de sequência – uma série de números naturais que correspondem a um número real. Existem alguns tipos delas, sendo que os mais conhecidos são a Progressão Aritmética e a Progressão Geométrica.
Em uma sequência, o termo é dado como ?n, sendo que n equivale à posição do termo e é sempre um número natural. De forma que a notação da sequência se apresenta da seguinte forma:
(?1,?2,?3,…,?n)
Uma sequência pode ser tanto finita quanto infinita. No segundo caso, a sequência será apresentada com três pontos no final.
As sequências seguem uma lógica, chamada de Lei de Formação. Ela permite calcular qualquer termo de uma sequência levando em conta a posição dele, ou seja, o n.
Como exemplo, podemos usar a famosa Sequência de Fibonacci. Nela, um termo é sempre resultado da soma dos dois anteriores. Assim, podemos escrever a Lei de Formação da seguinte forma:
?n = ?n-1 + ?n-2, ? ≥ 3
Portanto, se eu quero saber o quinto número da sequência de Fibonacci, preciso calcular F5 = F4 + F3.
O que é uma Progressão Aritmética?
Agora, quando falamos de uma PA, nos referimos a uma sequência que tem como lei de formação a seguinte fórmula:
?1 = ?
?n = ?n-1 + ?
A diferença entre um termo e seu antecessor é sempre a mesma. Ou seja, você sempre soma o mesmo valor para obter o número seguinte da sequência. Esse valor é chamado de razão e é representado pelo r.
Ficou confuso? Confira alguns exemplos:
- (1, 2, 3, 4, 5, 6, 7). Essa sequência é uma PA de razão ? = 1, pois:
?2 − ?1 = 2 − 1 = 1
?3 − ?2 = 3 − 2 = 1
?4 − ?3 = 4 − 3 = 1
?5 − ?4 = 5 − 4 = 1
?6 − ?5 = 6 − 5 = 1
?7 − ?6 = 7 − 6 = 1
Perceba que essa sequência segue a lei de formação:
?n = ?n-1 + 1
- (− 4, 0, 4). PA de razão ? = 4.
?2 − ?1 = 0 − (− 4) = 4
?3 − ?2 = 4 − 0 = 4
Como encontrar o Termo Geral da PA?
Há uma forma de descobrir um termo de uma PA apenas pela posição que ele ocupa? Sim! Fazemos isso calculando o termo geral da PA por meio da fórmula de recorrência. Entenda o raciocínio:
?2 = ?1 + ?
?3 = ?2 + ?
?4 = ?3 + ?
⋮
?n = ?n-1 + ?
Se somar todos os termos de uma PA, obtemos:
?2 + ?3 + ?4 + … + ?n = ?1 + ?2 + ?3 + … + ?n-1 + (? − 1) ?
Os termos em negrito se cancelam, o que permanece é o que chamamos de termo geral da PA:
?n = ?1 + (? − ?) ?
Tipos de PA
Uma PA pode ser classificada em PA crescente, PA constante e PA decrescente. O que determina o tipo de uma PA é a sua razão (r).
Então, se r > 0, a PA é crescente. Ou seja, os números da sequência aumentam progressivamente, como em (2,6,10,14,18).
Se r = 0, a PA é constante e todos os números da sequência são iguais. Exemplo: (3,3,3,3,3,3).
Se r < 0, a PA é decrescente. Um exemplo seria uma sequência com r = – 5, que resultaria em algo como (10, 5, 0, -5, -10).
Quais são as Propriedades da PA?
Uma PA possui algumas propriedades que facilitam na hora de encontrar os resultados procurados.
Termos Equidistantes
A primeira das propriedades diz que a soma de dois termos equidistantes dos extremos de uma PA é igual à soma dos extremos ?1 + ?n . Ou seja:
?1 + ?n = ?2 + ?n-1 = ?3 + ?n-2 =…= ?j+1 + ?n-j
Para você saber se os termos são equidistantes, some os índices e veja se o resultado é igual a 1+n. Exemplo:
?1 + ?n ⇒ ???? ??? í?????? = 1 + ?
?2 + ?n-1 ⇒ ???? ??? í?????? = 2 + (? − 1) = 1 + ?
?j+1 + ?n-j ⇒ ???? ??? í?????? = (? + 1) + (? − ?) = 1 + ?
Agora, vamos demonstrar essa propriedade. Suponha ?∈ℕ e ? > 1, vamos escrever ?j+1 + ?n-j usando o termo geral da PA.
?? = ?1 + (? − 1) ?
??+1 = ?1 + ((? + 1) − 1) ? = ?1 + ??
??−? = ?1 + [(? − ?) − 1] ?
??+1 + ??−? = ?1 + ?? + {?1 + [(? − ?) − 1] ?}
??+1 + ??−? = ?1 + ?? + ?1 + ?? − ?? − ?
??+1 + ??−? = ?1 + ?1 + ?? − ?
??+1 + ??−? = ?1 + ?1 + (? − 1) ?
Perceba que ?? = ?1 + (? − 1) ?. Substituindo na equação, obtemos:
??+1 + ??−? = ?1 + ??
Portanto provamos que para qualquer ?∈ℕ e ? > 1, a soma dos termos equidistantes resulta em um número constante (?1 + ??).
Soma dos termos
É possível calcular a soma de todos os termos de uma PA com a seguinte fórmula:
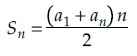
Para chegar nessa fórmula, escrevemos ?? como a soma de todos os ? termos de uma PA:
?? = ?1 + ?2 + … + ??−1 + ??
Também podemos escrever a soma ??, invertendo a ordem dos termos:
?? = ?? + ??−1 + … + ?2 + ?1
Somando essas duas equações e juntando os termos equidistantes:
2?? = (?1 + ??) + (?2 + ??−1) + … + (??−1 + ?2) + (?? + ?1)
Pela propriedade dos termos equidistantes da PA, vamos escrever as somas em função de (?1 + ??):
2?? = (?1 + ??) ?
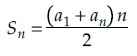
Quando uma PA tem uma quantidade ímpar de termos, é possível calcular Sn a partir da multiplicação do termo do meio da sequência pelo n. A fórmula é a seguinte:
Chegamos nela desta forma:
Usando o termo geral da PA, temos:
?? = ?1 + (? − 1) ?
Calculando ?1 + ??:
?1 + ?? = ?1 + ?1 + (? − 1) ?
?1 + ?? = 2?1 + (? − 1) ?
Dividindo por 2:
Logo, para ? ímpar:
Tome nota!
A soma dos ? termos de uma sequência também pode ser representada dessa forma:
Σ é o símbolo usado para representar um somatório.
O índice ? abaixo desse símbolo indica o primeiro termo do somatório e o índice ? indica até qual índice vai o somatório.
Exemplo:
Média Aritmética
Essa propriedade é muito útil para resolução de diversas questões envolvendo PA, pois conseguimos expressar os termos sem usar a razão (r). Isso facilita os cálculos. A fórmula da Média aritmética é a seguinte:
Para exemplificar, observe a demonstração. Vamos escrever ??−1 e ??+1, usando o termo geral:
??−1 = ?1 + ((? − 1) − 1) ? = ?1 + (? − 2) ?
??+1 = ?1 +(( ? + 1) − 1) ? = ?1 + ??
Somando os dois termos, obtemos:
??−1 + ??+1 = [?1 + (? − 2) ?] + (?1 + ??)
??−1 + ??+1 = ?1 + ?? − 2? + ?1 + ??
??−1 + ??+1 = 2 ?1 + 2?? − 2?
??−1 + ??+1 = 2 [?1 + (? − 1) ?]
?? = ?1 + (? − 1) ? ⇒ ??−1 + ??+1 = 2??
Um termo de uma PA pode ser escrito como a média dos seus termos vizinhos. Para a prova, grave: se tivermos uma PA (?1,?2,?3), podemos escrever ?2 como a média aritmética de ?1 e ?3:
Notação especial
Essa propriedade é útil para facilitar os cálculos de problemas envolvendo PA. A ideia é representar seus termos em função de um ? e ?, como demonstrado abaixo.
PA com 3 termos:
(? − ?, ?, ? + ?)
PA com 4 termos. Note que, neste caso, a razão pode ser dada como ? = 2?′.
(? − ??′, ? − ?′, ? + ?′, ? + ??′)
PA com 5 termos:
(? − ??, ? − ?, ?, ? + ?, ? + ??)
Hora de praticar!
Agora que você sabe o básico sobre sequências e PA, que tal treinar um pouco seus conhecimentos? Resolva o exercício abaixo!
Dado ?? = ? e ? = ?, o primeiro termo e a razão de uma PA, respectivamente. Calcule:
a) ???
b) ???
Resolução:
a) ?10
Temos os dados do primeiro termo e a razão da PA. Vamos usar o termo geral da PA para calcular ?10:
?? = ?1 + (? − 1) ?
?10 = 3 + (10 − 1)
5?10 = 3 + 9∙5
?10 = 48
b) ?20
?? = ?1 + (? − 1) ?
?20 = 3 + (20 − 1) 5
?20 = 3 + 19∙5
?20 = 98
Gostou do conteúdo? Acompanhe o Portal do Estratégia Militares e tenha acesso a mais resumos dos nossos professores! Além disso, se quiser treinar ainda mais seus conhecimentos, assine o Banco de Questões do Estratégia Militares! São milhares de questões dos mais variados níveis, tanto inéditas quanto de concursos anteriores, para você aproveitar! Clique no banner e saiba mais!




