Já ouviu falar no Movimento Circular Uniforme (MCU)? Ele é realizado por um ponto material percorrendo uma circunferência de raio R em movimento uniforme. Isso quer dizer que o ponto material varre ângulos iguais em intervalos de tempos iguais.
Dessa forma, dizemos que o MCU é periódico, pois, a cada volta completada pelo móvel, as características do movimento se repetem em intervalos de tempo iguais.
Quer saber mais sobre esse assunto que pode cair em uma prova de Concursos Militares? Confira a seguir com o Estratégia Militares.
Navegue pelo conteúdo
Período e frequência
Define-se período, representado pela letra t, como sendo o intervalo de tempo mínimo para o movimento repetir-se com as mesmas características.
Por exemplo, no MCU, o período é o intervalo de tempo em que o ponto material leva para percorrer uma volta completa. Ou seja, se ele leva 0,5 s para realizar uma volta no MCU, seu período é dado por: 𝑇 = 0,5 𝑠.
De forma correlacionada, define-se frequência como sendo o número de vezes que o movimento se repete na unidade de tempo. Ou seja:
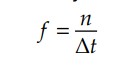
Onde: 𝑛 é o número de repetições e Δ𝑡, o intervalo de tempo considerado.
Para o MCU, 𝑓 é o número de voltas – ou ciclos – que o ponto material realiza na unidade de tempo. Por exemplo, se uma partícula completa 5 voltas em 10 segundos, então, sua frequência será:
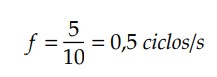
A unidade de ciclos/s recebe o nome de hertz, descrita por 𝐻𝑧. Esta é a unidade de frequência. Logo, dizemos que nossa frequência do exemplo é de 0,5 𝐻𝑧.
Em alguns lugares, aparece o termo “cada volta” para denominar rotação. Por isso encontramos em alguns lugares o termo 𝑟𝑝𝑠 (rotações por segundo), outro nome para unidade hertz.
Diante da definição de período e de frequência, podemos encontrar uma relação entre as duas grandezas, por uma regra de três simples e direta:

Essa relação é extremamente importante no estudo de movimentos periódicos. No exemplo anterior, para uma frequência de 0,5 𝐻𝑧, o período é de:
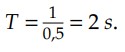
Apesar da unidade de frequência ser hertz (𝐻𝑧), é comum aparecer a unidade rotações por minuto (𝑟𝑝𝑚). A relação entre as unidades é dada por:
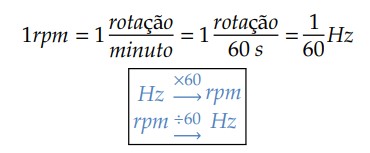
Com isso, podemos relacionar período e frequência com as velocidades do ponto material no MCU. Para uma volta completa, o espaço angular do móvel foi de 2𝜋 e o intervalo de tempo corresponde ao período 𝑇. Logo:
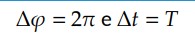
Portanto, podemos escrever a velocidade angular em função do período ou em função da frequência:
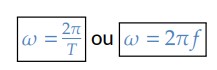
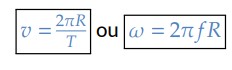
Como 𝑣 = 𝜔.𝑅, podemos escrever a velocidade linear como:
Função horária do espaço angular
Considere um móvel realizando um MCU, no sentido anti-horário, como visto abaixo:
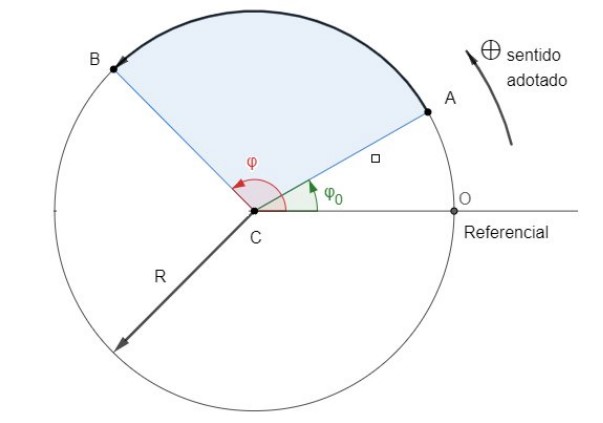
Como característica deste movimento, a velocidade escalar linear é constante, portanto:
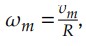
Assim, concluímos que a velocidade escalar angular também é constante. Logo:
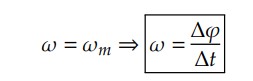
Se no instante 𝑡0 (início do movimento) o ponto material está no espaço angular 𝜑0 e, em um instante qualquer 𝑡, o ponto material tem espaço angular 𝜑, então:
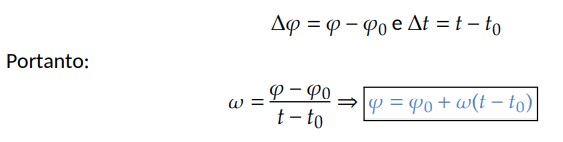
Para simplificar a expressão, vamos começar a contabilizar o início do movimento na origem dos tempos, isto é, 𝑡0 = 0, temos que:
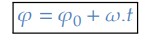
Como esperado, a função horária do espaço angular no MCU é uma expressão do primeiro grau em 𝑡, onde:
- 𝜑0 é o espaço angular inicial quando 𝑡 = 0;
- 𝜔 é a velocidade escalar angular instantânea (𝜔 ≠ 0); e
- 𝜑0 e 𝜔 são valores constantes.
De imediato, como 𝜔𝑚 = 𝜔, dizemos que a velocidade escalar angular não varia, ou seja, dizemos que neste movimento não existe aceleração escalar angular (𝛾 = 0).
Outra forma de obter a função horária do espaço angular é dividir a função horária do espaço linear pelo raio da circunferência onde o móvel descreve o MCU:
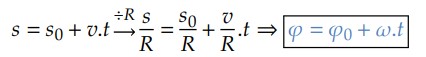
Gostou desse conteúdo? Agora que você entendeu tudo sobre o MCU, conheça os cursos do Estratégia Militares. Nosso material totalmente voltado para os Concursos Militares vai ajudar você a conquistar sua tão sonhada vaga nas Forças Armadas. Clique no banner e saiba mais!
Conteúdo didático elaborado pelo professor Toni Burgatto.



